線形代数¶
線形代数は、線形空間における代数の学問ですが、ここでは、NumPyのベクトルや行列についても紹介します。
Pythonでは NumPy を使って 多次元配列 を表現できます。NumPyの多次元配列では、各次元によって次のような言葉を使います。「NumPyの用語や計算」が数学の定義と異なる場合、本ページでは「NumPyのベクトル」のように記述します。
多次元配列の次元 |
言葉 |
|---|---|
0 |
スカラー |
1 |
ベクトル |
2 |
行列 |
3以上 |
テンソル(広義には0次元以上) |
スカラー は「1つの数値」を「ベクトルや行列」と対比させた言い方ですが、NumPyのスカラーは「整数や浮動小数点数」とは別の多次元配列です。以降では、NumPyのスカラーは用いません。スカラーという場合、「1つの数字」という意味です。
ベクトル¶
ベクトル とは、 (139.75, 35.68) のように、数字の並びを丸括弧でくくったものです。要素数をベクトルの次元といいます(多次元配列の次元とは別の概念です)。 (5, 2, 7) は3次元ベクトルです。N次元ベクトルをN次元空間で表現するとき、矢印を使います。ベクトルの要素は、矢印の各軸の増加量で表します。例えば、 (1, 2) は下図のようになります。

ベクトル \(v\) のi番目の要素を \(v_i\) と記述します。すなわち、N次元ベクトルの場合、 \(v = (v_1, v_2, \cdots, v_n)\) です。ベクトルであることを示すために、 \(\vec{v}\) のように記述することもあります。
NumPyのベクトルは、 numpy.array([1, 2]) のように記述します。 v がNumPyのベクトルのとき、i番目の要素は v[i - 1] です。
単位ベクトル¶
単位ベクトルは、ノルム(後述)が1のベクトルです。 \(e\) と記述することが多いです。
零ベクトル¶
全要素が0のベクトルです。ゼロベクトルともいいます。 \(\vec{0}\) や \(0\) と記述します。
NumPyのN次元零ベクトルは、 numpy.zeros(N) です。
行列¶
行列 とは、下図のように縦方向(行)と横方向(列)に数字がならんだ構造です。N行M列の行列をN×M行列といいます。 \(\begin{pmatrix} 3 & 1 & 4 \\ 1 & 7 & 3 \end{pmatrix}\) は2×3行列です。
NumPyの行列は、 numpy.array([[3, 1, 4], [1, 7, 3]]) のように記述します。 m がNumPyの行列のとき、i行目j列目の要素は m[i - 1, j - 1] です。
正方行列¶
N×N行列をN次正方行列または単に 正方行列 といいます。
単位行列¶
正方行列 \(A\) において、対角要素が1で、それ以外が0であるとき、行列 \(A\) を 単位行列 といいます。 \(I\) と記述することが多いです(以降、 \(I\) を単位行列とします)。
NumPyでは、 numpy.eye(N) で、N×N単位行列を作成できます。
零行列¶
全要素が0の行列です。ゼロ行列ともいいます。 \(O\) と記述します。
NumPyでは、 numpy.zeros((N, N)) で、N×N零行列を作成できます。
逆行列¶
正方行列 \(A\) と \(B\) に対し、 \(A B = I\) となる \(B\) を \(A\) の逆行列といい、 \(A^{-1}\) と表します。 \(AB\) は \(A\) と \(B\) の積(後述)です。
NumPyでは、 numpy.linalg.inv(A) で計算できます。
転置¶
要素と軸の対応を反転することを 転置 といいます。 \(A\) を行列としたとき、「i行目j列目の要素をAのj行目i列目の要素とした行列」を \(A\) の転置行列といい、 \(A^T\) と記述します。 また、 \(A^T = A\) となる行列を 対称行列 といいます。
N×1行列、1×N行列を、それぞれ列ベクトルと行ベクトルといいます。このとき、列ベクトルの転置ベクトルは、行ベクトルになります。ただし、列ベクトルや行ベクトルを単にベクトルと呼ぶこともあります。
なお、NumPyでは、列ベクトルや行ベクトルは行列として作成します。NumPyの転置も A^T と記述します。
行列のランク¶
行列のランク は、一次独立な行ベクトルの最大本数です。 階数 とも呼ばれます。
NumPyでは、 numpy.linalg.matrix_rank で計算できます。
「 \(v, w\) が一次独立」とは、「 \(v, w\) がどちらも零ベクトルでなく、内積(後述)が0」ということです。
行列のノルム¶
行列ノルム は、ベクトルのノルムを行列に対し自然に一般化したものです。
NumPyでは、 numpy.linalg.norm で計算できます。
固有値と固有ベクトル¶
\(A x = \lambda x\) となる零でないベクトル \(x\) とスカラー \(\lambda\) が存在するとき、 \(x\) を \(A\) の 固有ベクトル 、 \(\lambda\) をAの 固有値 といいます。
NumPyでは、 numpy.linalg.eig で計算できます。
行列式¶
行列式 正方行列に対して計算でき、 \(|A|\) あるいは \(\det{A}\) と表記されます。
NumPyでは、 numpy.linalg.det で計算できます。 \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\) の行列式は、 a * d - b * c になります。
行列式は、全ての固有値を掛けた値と等しく、行列式が0だと逆行列は存在しません。
演算¶
ベクトルの演算¶
\(\alpha\) をスカラー、 \(v = (v_1, v_2, \cdots, v_n), w = (w_1, w_2, \cdots, w_n)\) をベクトルとしたとき、以下のように計算します。
\(v + \alpha = (v_1 + \alpha, v_2 + \alpha, \cdots, v_n + \alpha)\)
\(v - \alpha = (v_1 - \alpha, v_2 - \alpha, \cdots, v_n - \alpha)\)
\(\alpha v = (v_1 \times \alpha, v_2 \times \alpha, \cdots, v_n \times \alpha)\)
\(v + w = (v_1 + w_1, v_2 + w_2, \cdots, v_n + w_n)\)
\(v - w = (v_1 - w_1, v_2 - w_2, \cdots, v_n - w_n)\)
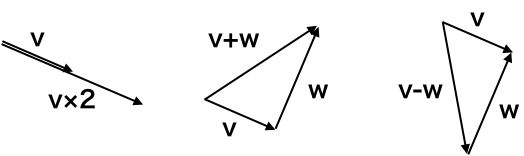
NumPyのベクトルも同様に計算できます。
ベクトル
v * 2は、ベクトルvを2倍に伸ばしたものになります。ベクトル
v + wは、vの先からwの分さらに進んだものになります。ベクトル
v - wは、vの先からwの分、逆向きに進んだものになります。
\(v \cdot w\) をベクトルの 内積 といい、 \(v_1 \times w_1 + v_2 \times w_2 + \cdots + v_n \times w_n\) で計算します。結果はスカラーになるので、スカラー積ともいいます。 \(v, w\) が列ベクトルの場合、 \(v^T w\) と書くこともあります。
NumPyでは、 numpy.dot(v, w) または v @ w で内積を計算できます。
ノルム は、ベクトルの大きさを概念です。主なノルムを以下に示します。
\(L^2\) ノルム: \(\|v\|_2 = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}\)
\(L^1\) ノルム: \(\|v\|_1 = |v_1| + |v_2| + \cdots + |v_n|\)
※ ノルムを距離と捉えた場合、 \(L^2\) ノルムをユークリッド距離(いわゆる距離)、 \(L^1\) ノルムをマンハッタン距離ともいいます。 \(L^2\) ノルムは、単に \(\|v\|\) と書くこともあります。
内積は、ベクトルの間の角 \(\theta\) と \(L^2\) ノルムを使って \(v \cdot w = \cos \theta \|v\| \|w\|\) で計算できます。
NumPyでは、 \(L^2\) ノルムを np.linalg.norm(v) 、 \(L^1\) ノルムを np.linalg.norm(v, 1) で計算できます。
行列の演算¶
\(\alpha\) をスカラー、 \(A = \begin{pmatrix} a_{11} & a_{12} & \cdots \\ a_{21} & a_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) 、 \(B = \begin{pmatrix} b_{11} & b_{12} & \cdots \\ b_{21} & b_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) を行列としたとき、以下のように計算します。
\(\alpha A = \begin{pmatrix} a_{11} \times \alpha & a_{12} \times \alpha & \cdots \\ a_{21} \times \alpha & a_{22} \times \alpha & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\)
\(A + B = \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \cdots \\ a_{21} + b_{21} & a_{22} + b_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\)
\(A - B = \begin{pmatrix} a_{11} - b_{11} & a_{12} - b_{12} & \cdots \\ a_{21} - b_{21} & a_{22} - b_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\)
NumPyでは通常の式のように書けます。
サンプルコード
α = 2
A = numpy.array([[10, 20], [30, 40]])
B = numpy.array([[1, 2], [3, 4]])
print(α * A)
print(A + B)
print(A - B)
出力
[[20 40]
[60 80]]
[[11 22]
[33 44]]
[[ 9 18]
[27 36]]
なお、NumPyに限り、 A + α や α + A も計算可能で、全要素にαを足した多次元配列になります。 詳しくは、 ブロードキャスト を参照ください。
行列とベクトルの積¶
\(v = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \end{pmatrix}\) 、 \(A = \begin{pmatrix} a_{11} & a_{12} & \cdots \\ a_{21} & a_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) としたとき、以下のように計算します。
\(A ~ v = \begin{pmatrix} a_{11} \times v_1 + a_{12} \times v_2 + \cdots \\ a_{21} \times v_1 + a_{22} \times v_2 + \cdots \\ \vdots \end{pmatrix}\)
\(v^T A = \begin{pmatrix} a_{11} \times v_1 + a_{21} \times v_2 + \cdots \\ a_{12} \times v_1 + a_{22} \times v_2 + \cdots \\ \vdots \end{pmatrix}\)
NumPyでは @ を使います。 * は、別の計算になるので注意してください。
サンプルコード
v = numpy.array([1, -1])
A = numpy.array([[5, 2], [3, 1]])
print(A @ v) # [3 2]
print(v @ A) # [2 1]
行列の積¶
\(A = \begin{pmatrix} a_{11} & a_{12} & \cdots \\ a_{21} & a_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) 、 \(B = \begin{pmatrix} b_{11} & b_{12} & \cdots \\ b_{21} & b_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) としたとき、以下のように計算します。
\(A ~ B = \begin{pmatrix} \sum_i{a_{1i} b_{i1}} & \sum_i{a_{1i} b_{i2}} & \cdots \\ \sum_i{a_{2i} b_{i1}} & \sum_i{a_{2i} b_{i2}} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\)
NumPyでは @ を使います。 * は、要素ごとの掛け算になるので注意してください。
サンプルコード
A = numpy.array([[1, -1], [-1, 3]])
B = numpy.array([[5, 2], [3, 1]])
print(A @ B)
出力
[[2 1]
[4 1]]
これは、下記のように計算しています。
[[ 1*5-1*3 1*2-1*1]
[-1*5+3*3 -1*2+3*1]]
M×L行列 \(A\) とL×N行列 \(B\) の積 \(A B\) は、M×N行列になります。たとえば、下記のように10×50行列と50×20行列の積は、10×20行列になります。
print((np.zeros((10, 50)) @ np.zeros((50, 20))).shape) # 10, 20
連立一次方程式¶
\(A = \begin{pmatrix} a_{11} & a_{12} & \cdots \\ a_{21} & a_{22} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}\) 、 \(b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \end{pmatrix}\) としたとき、 \(A x = b\) となる変数 \(x\) を求めることを 連立一次方程式 を解くといいます。
NumPyでは、以下のように numpy.linalg.solve を使って計算できます。
b = numpy.array([1, -1])
A = numpy.array([[5, 2], [3, 1]])
x = numpy.linalg.solve(A, b)
print(A @ x) # [ 1. -1.]

