ブロードキャスト¶
NumPyの演算では、次元数やサイズの小さい方を複製してデータを揃えようとします。これをブロードキャストと呼びます。
ブロードキャストのしくみを説明します。ちょっと難しいですが、これを理解すればどんな多次元配列でも計算できるようになります。
ブロードキャストの考え方¶
変数
data1と、次元数が同じか小さい変数data2を考えます。data1の次元数はn+k、data2の次元数はnとします(k >= 0)。shape1をdata1のshape = (m[1, 1], m[1, 2], …, m[1, n+k])とします。shape2をdata2のshape = (m[2, 1+k], m[2, 2+k], …, m[2, n+k])とします。shape2の頭にk個の1を追加してサイズがnになるようにします。shape2 = (m[2, 1], m[2, 2], …, m[2, n+k])(ただし、m[2, 1] = m[2, 1] = … = m[2, k] = 1)とします。
data1.shape == (3, 2, 4)の時、どのようになるか図で見てみましょう。
data2.shapeが (4, ), (2, 4), (3, 1, 4)の3ケースを表示します。
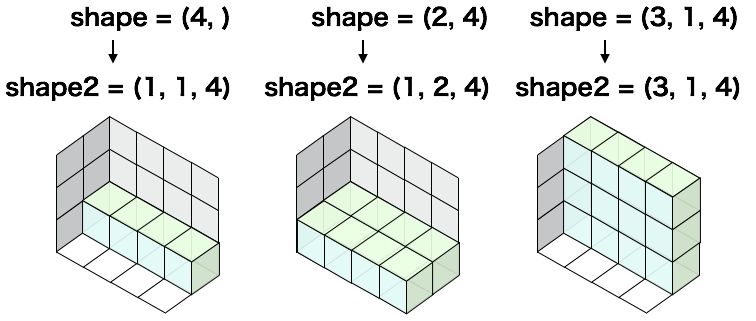
ブロードキャストの成立条件¶
ブロードキャストは、サイズが同じなるように伸ばします。
i = 1, 2, ..., n+kとなる全てのiに対し、m[1, i] == m[2, i] または m[1, i], m[2, i]のどちらかが1のとき、ブロードキャストできます。
逆にいうと、m[1, i] > 1 and m[2, i] > 1 and m[1, i] != m[2, i]となるiがあると、ブロードキャストできません。
先程の図で、この条件を満たしていることを確認してみましょう。
ブロードキャストでは、各次元ごとにサイズが同じになるように、足りなければ複製します。 複製といっても実際には、その時間やメモリーは使いません。
補足¶
多次元配列の片方が、全次元でサイズが大きくなくても構いません。
たとえば、shapeが(1, 3)と(2, 1)の場合も計算できます。
data1 = np.array([[1, 2, 4]])
data2 = np.array([[8], [16]])
print(data1 + data2)
上記は、下記のように表示されます。
[[ 9 10 12]
[17 18 20]]
代入¶
ブロードキャストして代入も比較と同じようにできますが、左辺の変数に[:]が必要です。
多次元配列の変数 = ...: 元の変数のアドレスとは別のアドレスに変わります(ブロードキャストされません)。多次元配列の変数[:] = ...: 元の変数のアドレスに新しいデータが代入されます(必要な時にブロードキャストされます)。
+=, *=, -=. /=, //=, %=などは、[:]を付けなくても大丈夫です。
変数のアドレスとは、変数が持っているデータが格納されている場所を識別するための値です。id(変数)で確認できます。

