基礎解析¶
本ページでは、解析の基礎として、微分、偏微分、定積分、不定積分を紹介します。
微分¶
時刻 \(t\) (sec)における「駅からの電車の位置」を \(f(t)\) (m)とします。ここでは、 \(f(t) = t^2 / 3\) とします。
Pythonで図示すると下図のようになります。
import numpy as np
import matplotlib.pyplot as plt
def f(t):
return t**2 / 3
t = np.linspace(0, 10)
plt.plot(t, f(t), label='$f(t) = t^2 / 3$')
plt.xlabel('t (sec)')
plt.ylabel('location (m)')
plt.legend();
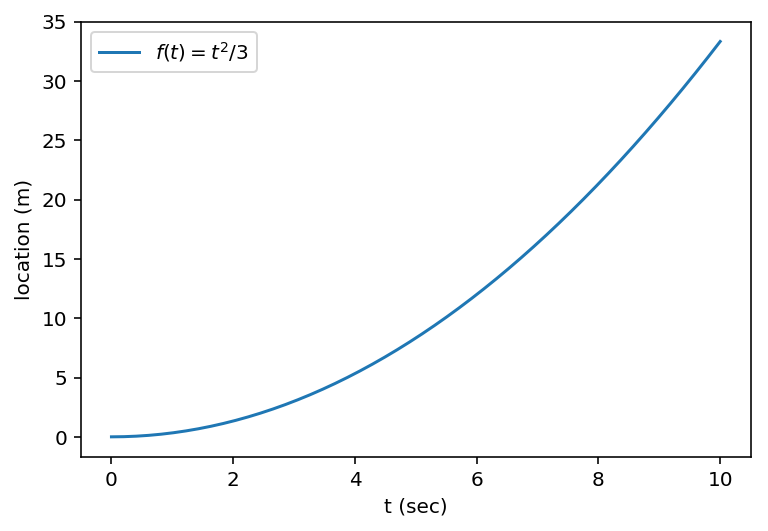
時刻 \(t\) の速度(m / sec)は、どうなるでしょうか?時刻 \(t\) から \(t + \epsilon\) の間に、位置は \(f(t)\) から \(f(t + \epsilon)\) になります。このときの速度は、距離÷時間で \((f(t+\epsilon) - f(t)) / \epsilon = ((t + \epsilon)^2 / 3 - t^2 / 3) / \epsilon = 2 t / 3 + \epsilon / 3\) と計算できます。 \(\epsilon\) を0に近づけていけば \(2 t / 3\) になると考えられます。
この変化を表す \(2t/3\) を求めることを 微分 するといいます。また、元の関数を 原始関数 といい、微分した関数を 導関数 といいます。 \(f(t)\) の導関数は \(f'(t)\) と記述します。
導関数は、原始関数の傾きを表しています。時刻6のときの接線の傾きは4です。グラフで確認してみましょう。
plt.plot(x, f(x))
plt.plot([3, 10], [0, 28]) # x = 6の接線
plt.plot([6, 6], [0, 35], 'k--', linewidth=1) # x = 6の点線
plt.xlabel('t (sec)')
plt.ylabel('location (m)');
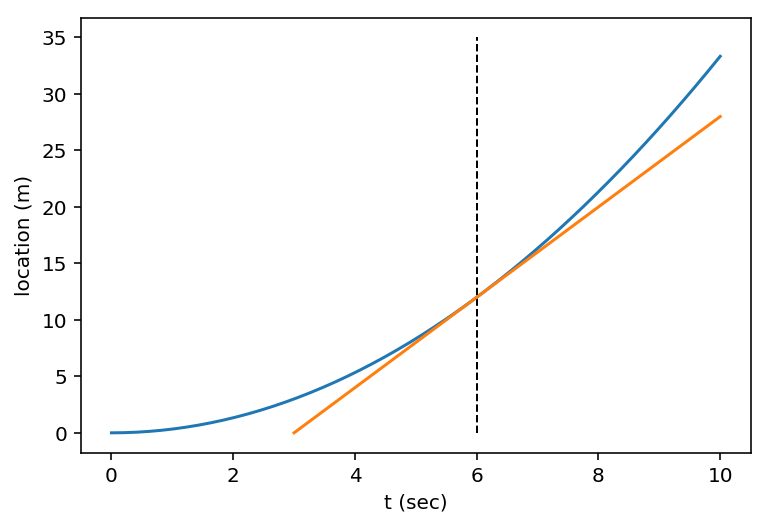
多項式を微分するときは、次のルールが使えます。
\(f(x) = x^n\) のとき、 \(f'(x) = n x^{n-1}\)
\(a\) を定数としたとき、 \((a f(x))' = a f'(x)\)
\(c\) を定数としたとき、 \(c' = (c x^0)' = 0\)
\((f(x) + g(x))' = f'(x) + g'(x)\)
たとえば、 \((3 x^2 - 4 x - 10)' = 6 x - 4\) になります。
また、距離を微分すると速度に、速度を微分すると加速度になります。
距離の例: \(t^2 / 3\)
速度の例: \(2 t / 3\)
加速度の例: \(2/3\)
偏微分¶
前節の原始関数では1つの変数を考えていました。 \(f(x, y) = x^2 y\) のように複数の変数がある関数の導関数を考えてみましょう。この場合、それぞれの変数ごとに微分を考えます。たとえば、 \(x\) で微分する場合は、残りの変数( \(y\) )を定数として扱います。このような微分を 偏微分 といい、以下のように記述します。
\(x\) で微分する場合: \(\frac{\partial f}{\partial x}(x, y)\)
\(y\) で微分する場合: \(\frac{\partial f}{\partial y}(x, y)\)
定積分¶
関数 \(f(x) = \sqrt{-x^2 + 2 x}\) を考えます。この関数は、座標 (1, 0) を中心とした半径1の半円になります。
この半円とX軸との間の面積を求めてみましょう。
Pythonでは下記のように、半円部分を描画できます。
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.sqrt(-x**2 + 2 * x)
x = np.linspace(0, 2, 300)
plt.fill_between(x, f(x));

この青い図形の面積は、 定積分 (definite integral)を使うと求められます。定積分は、 \(\int_0^2{f(x)} ~ dx\) のように記述します。これは「 \(f(x)\) について \(x\) が0から2までの加算した値」を意味します。
Pythonでは、SymPyまたはSciPyを使うと定積分を求められます。ここでは、SciPyの方法を説明します。
定積分の計算は、 scipy.integrate.quad(関数, 下限, 上限) を使います。返り値は、「定積分の値と推定誤差」です。
from scipy.integrate import quad
print(quad(f, 0, 2)) # 約(1.57, 1.00e-09)
不定積分¶
関数 \(f(x)\) に対して、 \(F'(x) = f(x)\) となる関数 \(F\) を求めることを 不定積分 (indefinite integral)といい、 \(F(x) = \int f(x) ~ dx\) と記述します。
Pythonでは、SymPyを使うと不定積分を求められますが、ここでは説明を省略します。

