数学の基礎知識

言葉

数学で用いられる言葉について紹介します。

言葉	意味
任意の \(x\) で \(\cdots\) が成り立つ	どのような \(x\) を想定しても、常に \(\cdots\) が成立することを意味します。
ある \(x\) で \(\cdots\) が成り立つ	\(\cdots\) が成立する特定の \(x\) が存在することを意味します。

Pythonで使える数値

Pythonで標準で使える数値には、以下の5種類があります。

種類	Pythonの例
整数	18, 0b10010, 0o22, 0x12
浮動小数点数	1.23
複素数	1+2j
十進浮動小数点数	decimal.Decimal('1.1')
有理数	fractions.Fraction(1, 2)

数値リテラルとしては、整数（int）、浮動小数点数（float）、複素数（complex）が利用できます。詳しくは、 数値リテラル を確認ください。

下記に、数値関連のPythonの組み込み関数を紹介します。

関数	Pythonの例	実行結果	説明
bin	bin(6)	'0b110'	数値を2進数表現の文字列に変換します。
complex	complex(1, 2)	1+2j	実部と虚部から複素数を作成します。
float	float('1.1')	1.1	数値や数値を表す文字列から浮動小数点数を作成します。
hex	hex(12)	0xc	数値を16進数表現の文字列に変換します。
int	int('110', 2)	6	数値や数値を表す文字列から整数を作成します。文字列の場合は、基数（N進数のN）を指定できます。
oct	oct(10)	0o12	数値を8進数表現の文字列に変換します。

また、 round を使うと「複素数以外の数値」を任意の桁で丸めることができます。丸めでは、端数が0.5のとき、対象桁の数字が奇数であれば切り上げ、偶数であれば切り捨てになります。 もし、浮動小数点数 x を小数点第一位で四捨五入したい場合は、int(x + 0.5) とします。

参考

• 組み込み関数

数学とPythonとの違い

数学と「Pythonの整数（int）や浮動小数点数（float）」には、以下の違いがあります。

数学	int	float
任意の数字が可能	（メモリの範囲で）無限桁数が可能	有限有効桁数、有限指数で可能
数字以外は計算の対象外	浮動小数点数との演算結果は、基本的に浮動小数点数になる	最大値、最小値、イプシロン※、非数、+無限大、-無限大を表せ、計算対象となる（ sys.float_info を参照）
数学のルールは成り立つ	数学のルールは成り立つ	数学のルールで規定されない演算もでき、桁落ちなどにより、数学のルールが成り立たないこともある
0割は許されない	0割は例外	0割は例外
無限大は数字ではない	無限大は表現できない	無限大も計算対象なので、他の数値と同様に扱える
非数は数字ではない	非数は表現できない	非数も計算対象なので、他の数値と同様に扱える

※ イプシロンは、「1より大きい最小の数と1との差」です。 計算機イプシロン を参考にしてください。

Pythonのfloatでは、無限大と非数を、 math.inf と math.nan で表現できます。演算結果は以下のようになります（ from math import inf, nan, isfinite, isinf, isnan, sin が必要）。

式	演算結果
nan == nan	False
nan != nan	True
isnan(nan)	True
inf == inf	True
isinf(inf) and isinf(-inf)	True
isfinite(inf) or isfinite(-inf) or isfinite(nan)	False
nan + 1	nan
nan * 0	nan
inf * 0	nan
inf + inf	inf
inf - inf	nan
inf / inf	nan
sin(nan)	nan

基本的にnanを使った演算はnanになります。特に、 math.nan == math.nan はFalseになるので、 math.isnan で判定する必要があります。

ギリシャ文字

数式ではギリシャ文字がよく使われます。ここでは、読み方を紹介します。

大文字	小文字	読み方
Α	α	アルファ
Β	β	ベータ
Γ	γ	ガンマ
Δ	δ	デルタ
Ε	ε	エプシロン・イプシロン
Ζ	ζ	ゼータ
Η	η	エータ・イータ
Θ	θ	テータ・シータ・セータ
Ι	ι	イオタ
Κ	κ	カッパ
Λ	λ	ラムダ
Μ	μ	ミュー
Ν	ν	ニュー
Ξ	ξ	クシー・クサイ・グザイ
Ο	ο	オミクロン
Π	π	パイ
Ρ	ρ	ロー
Σ	σ	シグマ
Τ	τ	タウ
Υ	υ	ユプシロン・ウプシロン
Φ	φ	ファイ
Χ	χ	キー・カイ
Ψ	ψ	プシー・プサイ
Ω	ω	オメガ

定数で使われる文字

数学で意味を持つ定数を 数学定数 といいます。ここでは、主なものを紹介します。Pythonでの記述では、 import math が必要です。

記号	名称	説明	Pythonでの記述	およその値
e	ネイピア数	自然対数の底	math.e	2.71828
π	円周率	円周／直径	math.pi	3.14159

集合

数学での記述

数学では、 集合 を {1, 2, 3} のように記述します。値 x が集合 A に含まれていることを、 x ∈ A と書きます。集合 A が集合 B に含まれていることを A ⊆ B と書きます。

Pythonでの記述

Pythonでは、集合は set を使います。Pythonで {1, 2, 3} と書くと set のリテラルになります。変数 x が集合 A に含まれていることを、 x in A と書きます。集合 A が集合 B に含まれていることを A <= B と書きます。

集合演算

集合の演算と set の演算の対応は以下のようになります（ A, B は集合です）。

演算の名前	記号	Pythonの記述	説明
和集合	A ∪ B	A｜B	A、Bのどちらかに含まれる要素の集合
積集合	A ∩ B	A & B	A、Bの両方に含まれる要素の集合
差集合	A ＼ B	A - B	Aに含まれてBに含まれない要素の集合
対称差	A Δ B	A ^ B	A、Bのどちらかだけに含まれる要素の集合

サンプルコード

A = {1, 2}
B = {2, 3}
print(1 in A)  # True
print({1} <= A)  # True
print(A | B)  # {1, 2, 3}
print(A & B)  # {2}
print(A - B)  # {1}
print(A ^ B)  # {1, 3}

論理演算

Pythonでは、はい/いいえ、Yes/No、OK/NG、On/Off、真/偽などの2値はブール型（ bool ）のブール値である True, False を使って表現できます。 主な論理演算とPythonの対応は以下のようになります（ P, Q は集合です）。

演算の名前	記号	Pythonの記述	説明
論理和	P ∧ Q	P and Q	PかつQ
論理積	P ∨ Q	P or Q	PまたはQ
否定	¬ P	not P	Pでない

サンプルコード

P = True
Q = False
print(P and Q)  # False
print(P or Q)  # True
print(not P)  # False

Pythonの and, or, not は、次のコードのようにブール値以外のオブジェクトで使えます（ただし、エラーを返す __bool__ を定義しているオブジェクトは除きます）。

print(0 and 123)  # 0
print(0 or 123)  # 123
print(123 or 456)  # 123
print('' or 'Hello')  # Hello
print(not 123)  # False

また、 and, or は短絡評価という機能もあります。詳細は 論理演算 - PyQドキュメント を参照ください。

数学記号

数学で使われる一部の記号を紹介します。

記号	例	説明
≒	\(x \fallingdotseq 1\)	ほとんど等しい（例は、xは1にほとんど等しい）
∀	\(\{x_i ~ \forall i \in N\}\)	任意の・全ての（例は、集合Nの全ての要素iに対して）
∃	\(f(x_i) = 0 ~ \exists i \in N\)	ある・少なくとも1つの（例は、集合Nのある要素iに対して）
√	\(\sqrt[n]{m}\)	べき根・ \(m^{\frac{1}{n}}\) （nが2のときは \(\sqrt{m}\) と書き、平方根）
Σ	\(\sum^n_{i=1}{x_i}\)	和（例は \(x_1 + x_2 + \cdots + x_n\) ）
Π	\(\prod^n_{i=1}{x_i}\)	積（例は \(x_1 \times x_2 \times \cdots \times x_n\) ）
∫	\(\int^1_{x=0}{x^2} dx\)	積分

参考

• 数学記号の表

色々な関数

ここでは、指数関数、対数関数、三角関数を紹介します。 PythonではmathライブラリーとNumPyから利用できます。mathの関数の引数は数値でないといけませんが、NumPyの関数の引数は多次元配列が使えます。多次元配列については、 多次元配列 - PyQドキュメント を参照ください。 また、mathの関数の引数は、整数や浮動小数点数でないといけませんが、NumPyの関数の引数は複素数も使えます。

指数関数

\(f(x) = e^{x}\) で表される関数を 指数関数 （exponential function）といいます。ここでeは、自然対数の底でネイピア数（≒2.71828）です。任意の正のaに対して、 \(f(x) = a^x\) を指数関数と呼ぶ場合もあります。 指数関数は、連続複利計算などで使われます。

意味	Pythonの関数
狭義の指数関数（ \(e^x\) ）	math.exp(x), numpy.exp(x)
一般の指数関数（ \(a^x\) ）	a**x, math.pow(a, x), numpy.power(a, x)

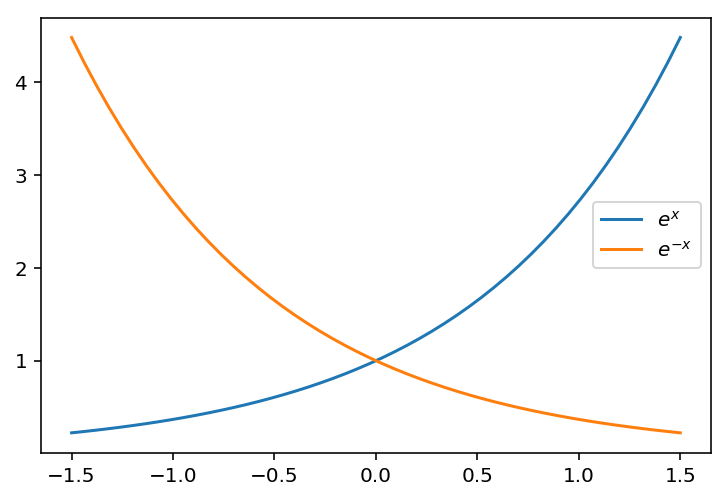
Pythonではmatplotlibを使って下記のように描画できます。

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1.5, 1.5)
plt.plot(x, np.exp(x), label='$e^x$')
plt.plot(x, np.exp(-x), label='$e^{-x}$')
plt.legend();

参考

• 指数関数

対数関数

\(x = a^y\) のとき、 \(y\) を「底を \(a\) とする \(x\) の 対数 」といい、 \(y = \log_a x\) と記述します。また、 \(\log\) を対数関数（logarithm function）といい、底が \(e\) の対数を自然対数（natural logarithm）といい、底が10の対数を常用対数（common logarithm）といいます。自然対数関数は \(\ln(y)\) とも記述し、指数関数の逆関数になります。

意味	Pythonの関数
自然対数関数	math.log(x)、numpy.log(x)
任意の底（base）の対数関数	math.log(x, base)、numpy.emath.logn(base, x)
常用対数関数	math.log10(x)、numpy.log10(x)

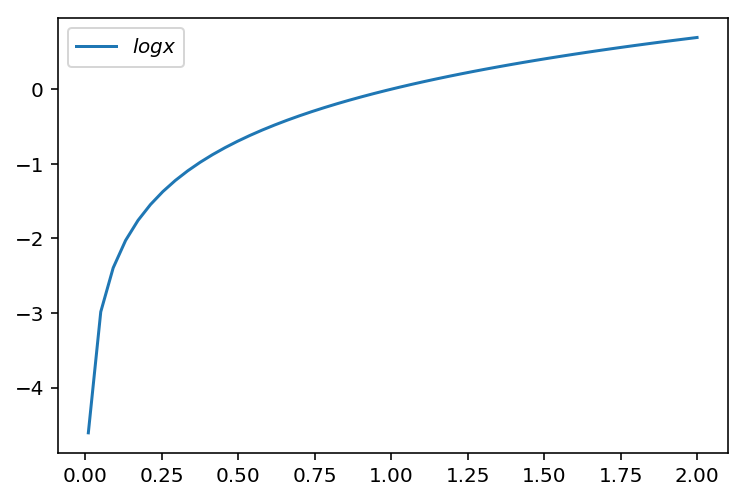
Pythonでは下記のように自然対数関数を描画できます。

x = np.linspace(0.01, 2)
plt.plot(x, np.log(x), label='$log x$')
plt.legend();

下記のように掛け算の対数が、対数の足し算になることが特徴です（ math.isclose は「ほぼ同じかどうか」を判定します）。昔の天文学や航海学の大きな数の計算で対数が用いられてきました。

from math import log, isclose
a, b = 123, 456
print(isclose(log(a * b), log(a) + log(b)))  # True

参考

• 対数

三角関数

直角三角形の1つの鋭角の角度（θとします）と「2辺の比」の関係を表す下記の関数を総称して三角関数といいます。古代から測量などで使われてきました。

名前	略称	Pythonの関数	2辺の比
サイン（sine、正弦）	sin	math.sin、numpy.sin	c/a
セカント（secant、正割）	sec	ー	a/b
タンジェント（tangent、正接）	tan	math.tan、numpy.tan	c/b
コサイン（cosine、余弦）	cos	math.cos、numpy.cos	b/a
コセカント（cosecant、余割）	csc, cosec	ー	a/c
コタンジェント（cotangent、余接）	cot	ー	b/c

「2辺の比」の「a, b, c」は下記を参照してください。

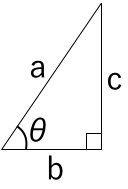
なお、 \(\sin \theta \times \sin \theta\) は、 \(\sin^2 \theta\) と記述します。

参考

• 三角関数

たとえば、θが「π/3」のとき、サインθ、コサインθ、タンジェントθは、Pythonで以下のようになります。mathライブラリーの三角関数の角度の単位はラジアンです（πラジアン = 180度）。なお、π（pi）は円周率（≒3.14159）です。

from math import pi, sin, cos, tan
θ = pi / 3
print(f'サインθ = {sin(θ):.4f}')  # サインθ = 0.8660
print(f'コサインθ = {cos(θ):.4f}')  # コサインθ = 0.5000
print(f'タンジェントθ = {tan(θ):.4f}')  # タンジェントθ = 1.7321

グラフは次のように書けます。

x = np.linspace(-pi, pi)
plt.xlim((-pi, pi))
plt.ylim((-1.1, 1.1))
plt.xticks(np.arange(-pi, pi + 0.01, pi / 2),
           ['-π', '-π/2', '0', 'π/2', 'π'])
plt.plot(x, np.sin(x), x, np.cos(x), x, np.tan(x))
plt.legend(['sin', 'cos', 'tan'])
plt.plot([-pi, pi], [0, 0], 'k:', linewidth=1)
plt.plot([0, 0], [-1.1, 1.1], 'k:', linewidth=1);

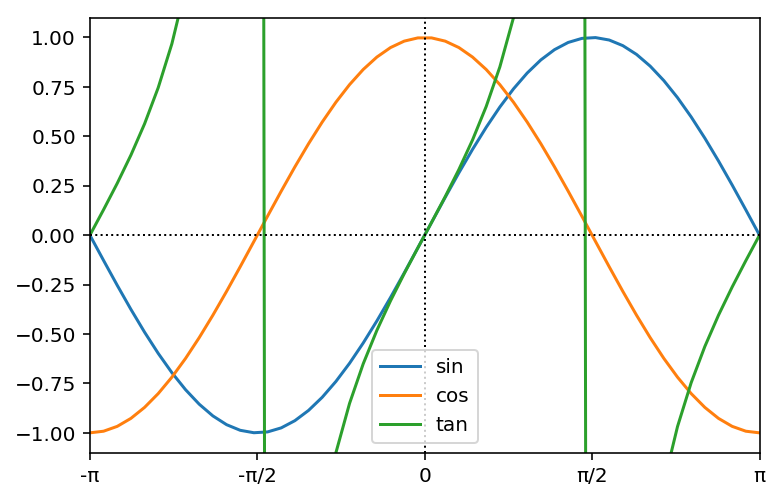
また、三角関数のθの範囲を -π / 2 から π / 2 に限ると、 sin と tan は逆関数を考えることができます。同様に 0 から π に限ると、 cos も逆関数を考えられます。

名前	Pythonの関数
サインの逆関数	math.asin、numpy.arcsin
コサインの逆関数	math.acos、numpy.arccos
タンジェントの逆関数	math.atan、math.atan2、numpy.arctan、numpy.arctan2

math.atan2(y, x), numpy.arctan2(y, x) は、 (-π / 2, π / 2) の範囲で math.atan2(y / x), numpy.arctan2(y / x) ですが、下記の点で優れています。

• 原点を中心とする円の円周上の点 (x, y) から360度の範囲（-πラジアンからπラジアン）の角度を求められます。

なお、 \(\arcsin \theta\) を \(\sin^{-1} \theta\) と記述します。

逆関数のグラフは次のように書けます。

x1 = np.linspace(-1, 1)
x2 = np.linspace(-3.5, 3.5)
plt.plot(x1, np.arcsin(x1), x1, np.arccos(x1), x2, np.arctan(x2))
plt.legend(['arcsin', 'arccos', 'arctan'])
plt.yticks(np.arange(-pi / 2, pi + 0.01, pi / 2), ['-π/2', '0', 'π/2', 'π'])
plt.hlines([-pi / 2, 0, pi / 2, pi], -3.5, 3.5, linestyle=':', linewidth=1)
plt.vlines([-1, 0, 1], -pi / 2, pi, linestyle=':', linewidth=1);

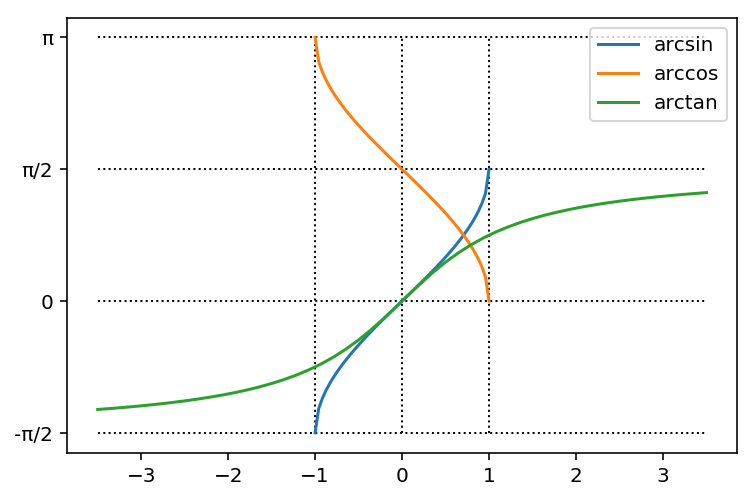
双曲線関数

以下の関数を双曲線関数といい、それぞれハイパボリックサイン、ハイパボリックコサイン、ハイパボリックタンジェントといいます。 \(\sinh x =\frac{e^x-e^{-x}}{2}\) \(\cosh x =\frac{e^x+e^{-x}}{2}\) \(\tanh x = \frac{\sin h}{\cos h}\)

名前	略称	Pythonの関数
ハイパボリックコサイン	sinh	math.sinh、numpy.sinh
ハイパボリックコサイン	cosh	math.cosh、numpy.cosh
ハイパボリックタンジェント	tanh	math.tanh、numpy.tanh

参考

• 双曲線関数

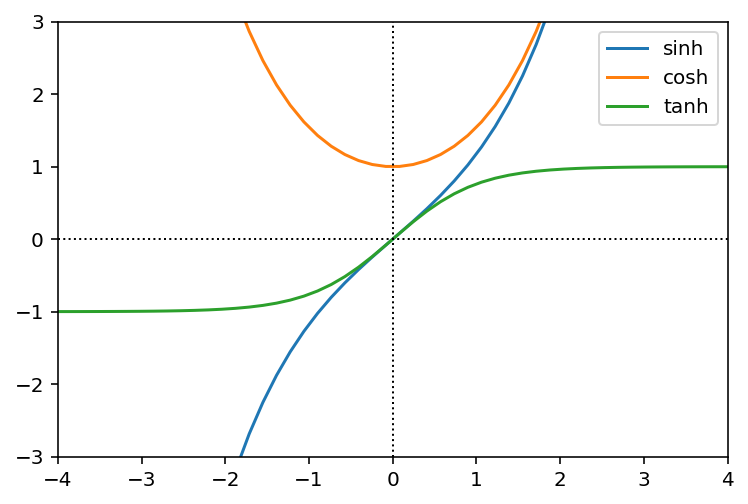
グラフは次のように書けます。

x = np.linspace(-4, 4)
plt.plot(x, np.sinh(x), x, np.cosh(x), x, np.tanh(x))
plt.xlim((-4, 4))
plt.ylim((-3, 3))
plt.legend(['sinh', 'cosh', 'tanh'])
plt.plot([-4, 4], [0, 0], 'k:', linewidth=1)
plt.plot([0, 0], [-3, 3], 'k:', linewidth=1);

当コンテンツの知的財産権は株式会社ビープラウドに所属します。詳しくは利用規約をご確認ください。