確率と統計¶

データと統計量¶

日本人の身長のデータを考えましょう。「日本人の身長のデータ」のように全データのことを、 母集団 といいます。また、「母集団から無作為に一部を取得したデータ」を標本といいます。データ分析では標本を対象とします（標本＝母集団の場合もあります）。

データの特徴を表す量を統計量といいます。ここでは、統計量の1つである 要約統計量 （代表値 ともいいます）を紹介します。要約統計量を見ることで、データの傾向を確認したり、複数のデータについて比較できます。

参考：要約統計量

Pythonでは要約統計量を色々なライブラリーで計算できますが、ここではNumPyとpandas（と一部SciPy）の計算方法を紹介します。データ（ \(a\) ）は、下記のように作成するものとします。また、データ数を \(N\) とし、各値を \(a_i\) とします。

import numpy as np
import pandas as pd
import scipy.stats

a = pd.Series([5, 2, 4, 9])
print(a.describe())  # 要約統計量一覧

平均¶

データの平均は、データの合計をデータ数で割ったものです。 \(\sum_i{a_i} / N\) になります。 np.mean(a) や a.mean() で計算できます。データのおおよその値を評価するのに使われます。

母集団の平均を母平均といい、標本の平均を標本平均といいます。標本平均の期待値（後述）は母平均になります。このように推定量の平均が真の値になるとき、 不偏推定量 といいます。

分散¶

データの分散は、「データから平均を引いて自乗した値」の平均です。平均を \(m\) としたとき、 \(\sum_i{(a_i - m)^2}/N\) になります。分散が大きくなると、データのばらつきが大きくなります。

母集団の分散を母分散といい、標本の分散を標本分散といいます。標本分散の平均は、母分散より小さくなります。

\(\sum_i{(a_i - m)^2}/(N-1)\) で計算される値は、母分散の不偏推定量になるので、不偏分散といいます。

母分散や標本分散は、 np.var(a) や a.var(ddof=0) で計算できます。

不偏分散は、 np.var(a, ddof=1) や a.var() で計算できます。

var では、分母を N - ddof としています。ただし、 ddof のデフォルトが、NumPyでは0ですが、pandasでは1になっています。

参考

標準偏差¶

標準偏差 は、分散の正の平方根です。データの単位が \(m\) の場合、分散の単位は \(m^2\) になります。標準偏差の単位は平均の単位と同じなので、分散より確認しやすいというメリットがあります。

母集団や標本の標準偏差は、 np.std(a) や a.std(ddof=0) で計算できます。

標準偏差の不偏推定量は、 np.std(a, ddof=1) や a.std() で計算できます。

歪度・尖度¶

歪度は、分布の左右非対称の度合いを表します。左右対称だと0に、右裾が長いと正に、左裾が長いと負になります。

尖度は、分布の尖り具合を表します（小さいとなだらか）。正規分布の尖度を0とします（3とする場合もあるので注意してください）。

母集団や標本の歪度は、 scipy.stats.skew(a) で計算できます。

歪度の不偏推定量は、 a.skew() や scipy.stats.skew(a, bias=False) で計算できます。

母集団や標本の尖度は、 scipy.stats.kurtosis(a) で計算できます。

尖度の不偏推定量は、 a.kurt() や scipy.stats.kurtosis(a, bias=False) で計算できます。

※ データに numpy.nan が含まれている場合、 scipy.stats.skew と scipy.stats.kurtosis に nan_policy='omit' をつけてください。

中央値¶

中央値 は、データを小さい順に並べたときの (N + 1) / 2 番目の値です。Nが偶数の場合は「 N / 2 番目の値と N / 2 + 1 番目の値」の平均です。メディアンともいいます。

中央値は、 a.median() や np.nanmedian(a) で計算できます。

四分位数¶

四分位数 は、データを小さい順に並べてデータ数を4分割した時の値を表しています。 25パーセンタイル値を第1四分位数、50パーセンタイル値を第2四分位数、75パーセンタイル値を第3四分位数といいます。第2四分位数は中央値と同じです。

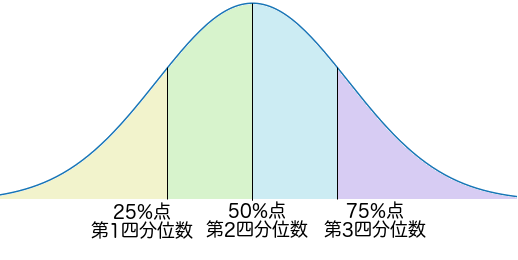
四分位数は、 a.describe()['25%':'75%'] や np.nanpercentile(a, [25, 50, 75]) で計算できます。

最小値・最大値¶

最小値・最大値は、データの最小の値と最大の値です。 | 最小値は、 a.min(), np.min(a) で計算できます。 | 最大値は、 a.max(), np.max(a) で計算できます。

最頻値¶

最頻値 は、データの度数分布（後述）で最も度数の高いビン（階級）の値です。モードともいいます。

最頻値は、データが離散値の場合は、 a.mode()[0] で計算できます。連続値の場合は、ビンを bins として collections.Counter(pd.cut(a, bins=bins)).most_common(1) で計算できます。

度数分布¶

年齢データ（ ages ）を考えます。

ages = [24, 31, 14, 27, 18, 25]
print(pd.value_counts(pd.cut(ages, range(10, 41, 10), False), False))

年代ごとの人数は、上記を実行して、下記のように出力されます。

［10, 20)    2
［20, 30)    3
［30, 40)    1
dtype: int64

このような結果を 度数分布 といいます。1列目をビン（階級）といい、2列目を度数といいます。ビン ［10, 20) は10歳以上20歳未満を意味します。

参考

相関係数と相関行列¶

組となる2つのデータ（ \(x, y\) ）についての以下の値を 共分散 といいます。ただし、 \(N, m_x, m_y\) は、それぞれデータ数と \(x, y\) の平均です。

\(s_{xy} = \frac{1}{N}\sum_i{(x_i - m_x)(y_i - m_y)}\)

また、 \(s_x, s_y\) をそれぞれ \(x, y\) の標準偏差としたとき、 \(r = \frac{s_{xy}}{s_x s_y}\) を 相関係数 （またはピアソンの積率相関係数）といいます。

複数のデータについて、各系列の相関係数を要素とする行列を 相関行列 といいます。相関行列は、対称行列で対角成分は1になります。

pandas.DataFrame.corr や numpy.corrcoef により、相関行列が計算できます。

参考

相関係数の目安¶

相関係数は-1〜1の値を取ります。
相関係数が正のとき、 正の相関 があるといい、散布図では右肩上がりの傾向を示します。
相関係数が負のとき、 負の相関 があるといい、散布図では右肩下がりの傾向を示します。

次表に、おおよその目安を示します。

相関係数の絶対値	意味	表現方法
0	相関なし	全く相関は見られなかった
0〜0.2	ほとんど相関なし	ほとんど相関が見られなかった
0.2〜0.4	低い相関あり	低い正（負）の相関が認められた
0.4〜0.7	相関あり	正（負）の相関が認められた
0.7〜1	高い相関あり	高い正（負）の相関が認められた
1	完全に相関	完全な正（負）の相関が認められた

相関係数は順序尺度になります。2つの相関係数が 0.3 と 0.6 になったときに2倍の相関があるとは言いません。

データの確認¶

報告書などでは、統計量を数値として盛り込むことが多いでしょう。しかし、数字だけだと直感的に把握しづらいです。ここでは、 matplotlib を使って視覚的にデータをとらえる方法を紹介します。

しばしば、誤解を生むようなグラフなどが使われることがあります。たとえば、3次元の円グラフは、手前の項目を大きく目立たせる効果があります。可視化は、正しく情報を伝えることを心がけましょう。「誤解を与える統計グラフ」も参考にしてください。

散布図¶

散布図 は、2つのデータの関連を図示するのに適しています。 plt.scatter などで表示できます。

参考

惑星ごとの自転周期（Rotation）と公転周期（Orbital）の関連を見てみましょう。どちらも大きな値含んでいます。以下では対数目盛にして、小さい値の違いをわかりやすくしています。

サンプルコード

planet = pd.DataFrame({
    'Rotation': [58.6, 243, 1, 1, 0.4, 0.4],
    'Orbital': [0.2, 0.6, 1, 1.9, 11.9, 29.5],
    'Name': 'Mercury Venus Earth Mars Jupiter Saturn'.split()
})
plt.scatter(planet.Rotation, planet.Orbital)
planet.apply(lambda row: plt.text(*row), 1)
plt.xlabel('Rotation period')
plt.ylabel('Orbital period')
plt.xscale('log')
plt.yscale('log');

ヒストグラム¶

ヒストグラム は、度数分布を棒グラフで表現したものです。ビン（階級）ごとに、そのビンに含まれるデータの個数（度数）を表示します。 plt.hist などで表示できます。

参考

サンプルコード

age_men = [10, 17, 21, 22, 25, 36]  # 男性の年齢のリスト
age_women = [11, 24, 31, 39] # 女性の年齢のリスト
plt.hist((age_men, age_women), bins=4, range=(0, 40));

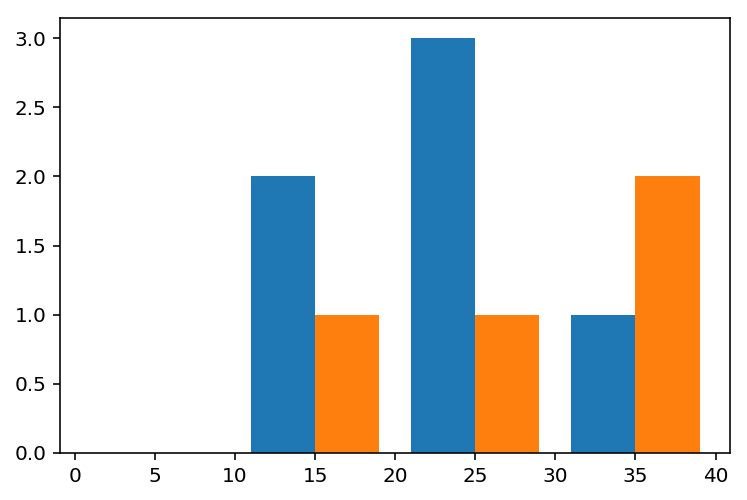
ビンの幅は、 range の幅を bins で割ったものです。この値をキリの良い数にするとヒストグラムが見やすくなります。

個々のヒストグラムではなく、全体のヒストグラムを見たい場合は、 stacked=True を使用すると積み上げヒストグラムになります。

散布図行列¶

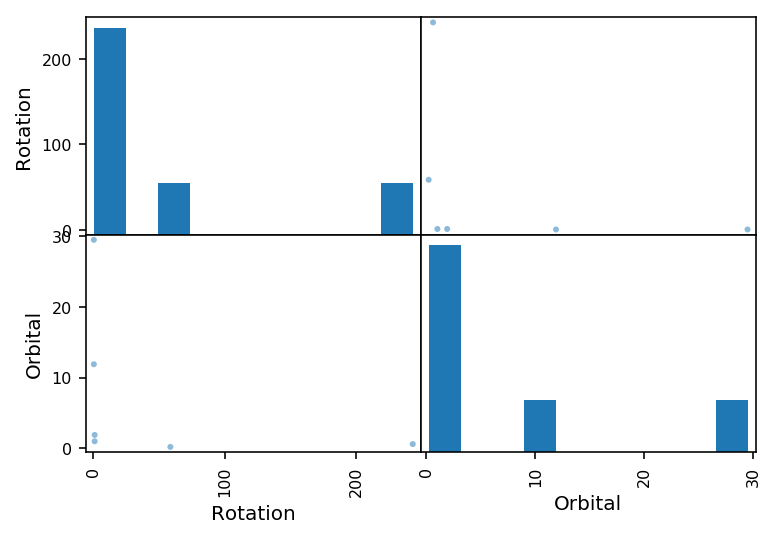
pandasでは、DataFrameの各列間の散布図とヒストグラムを一度に表示できます。これを 散布図行列 といいます。 pandas.plotting.scatter_matrix で表示できます。

参考

pandas.plotting.scatter_matrix

サンプルコード

pd.plotting.scatter_matrix(planet);

カーネル密度関数¶

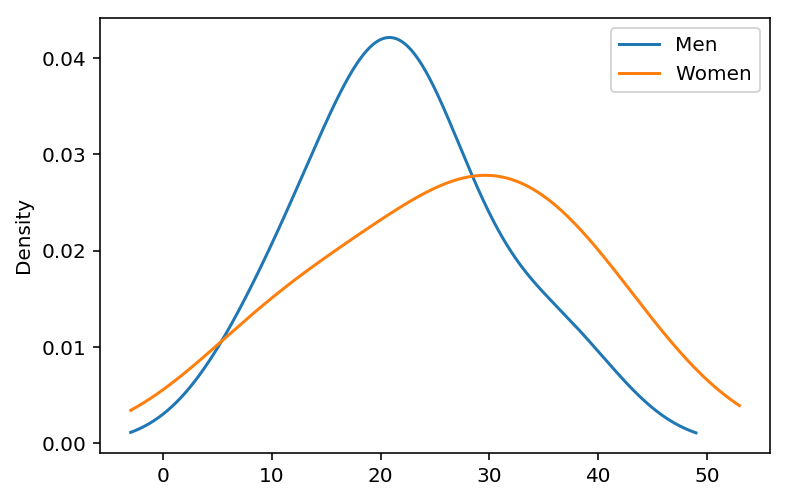
ヒストグラムでは、ビンの幅によって表示が異なります。ざっくりした分布を見たい場合、 カーネル密度関数 が使えます。カーネル密度関数は pandas.Series.plot.density で表示できます。

参考

サンプルコード

sr_age_men = pd.Series(age_men, name='Men')
sr_age_women = pd.Series(age_women, name='Women')
sr_age_men.plot.density()
sr_age_women.plot.density()
plt.legend();

箱ひげ図¶

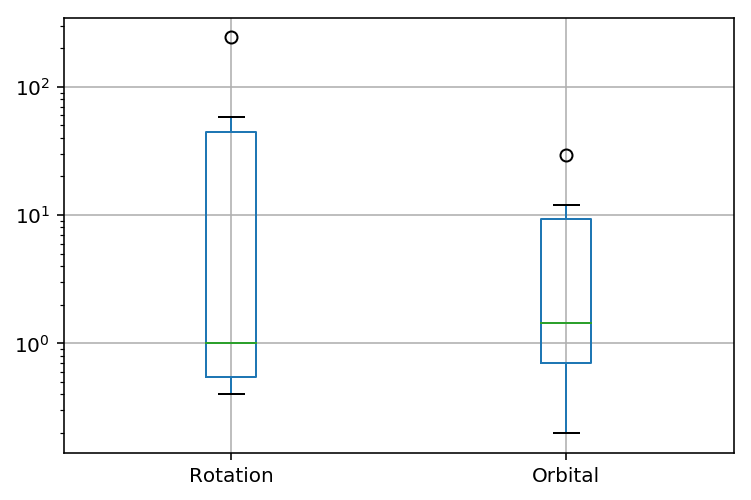
箱ひげ図 は、四分位数などを視覚的に確認するためのグラフです。 pandas.DataFrame.boxplot や plt.boxplot で表示できます。青の四角い箱の「下辺、緑の線、上辺」が、「第1四分位数、第2四分位数、第3四分位数」を表しています。○は外れ値を表しています。

参考

サンプルコード

plt.yscale('log')
planet.boxplot();

確率とは¶

サイコロを振ったところ1の目が出ました。これについて考えてみましょう。サイコロを振るようなことを数学の用語で試行といい、1の目が出るようなことを事象といい、事象の起こりやすさを確率（probability）といいます。サイコロは6個の目があります。いずれかの目が出るような事象を 全事象 といいます。全事象の起こる確率は1です。

どれも同じ起こりやすさとすると、1の目の出る確率は 1 / 6 と求められます。各事象の起こりやすさをきちんと把握することが大切です。宝くじを1枚買ったとき「当たるか当たらないかのどちらかだから、当たる確率は 1 / 2 になる」は正しくありません。

一般に、 \(P(\cdots)\) を使って確率を表します。

2つの事象 \(A, B\) があり、「 \(A\) と \(B\) が同時に起きる確率」と「 \(A\) が起きる確率× \(B\) の起きる確率」が等しい（ \(P(A \cap B) = P(A) P(B)\) である）とき、 \(A, B\) は独立であるといいます。

確率変数¶

事象に対し値を割り当てます。例えば、1の目が出たら1を2の目が出たら2とします。起こりうる事象の値を取りうる変数を 確率変数 （random variable）といいます。確率変数は、事象ごとの起こりやすさに比例してランダムな値を取ります。

たとえば、「サイコロを振ったときの目」を確率変数 \(X\) とすると「 \(X = 1\) 」は「1の目が出る事象」を表します。 \(P(X = 1)\) は、「1の目が出る確率」です。

確率変数を使った式も確率変数です。たとえば、 \(X + 1\) は「サイコロを振ったときの目に1を足した値」の確率確率に、 \(X * 2\) は「サイコロを振ったときの目を2倍した値」の確率確率になります。

期待値¶

確率変数の「値×確率」を全事象について和を取った値を 期待値 といい、 \(E[\cdots]\) で表します（ \(E(\cdots)\) と書くこともあります）。確率変数がある分布に従っている（後述）とき、期待値は分布の平均です。

「サイコロを振ったときの目」を確率変数 \(X\) としたとき、 \(E[X] = \sum_{i=1}^6{i * 1/6} = 21 / 6 = 3.5\) です。

分散¶

\(V[X] = E[(X - E[X])^2]\) を確率確率の分散といいます（ \(V(X)\) と書くこともあります）。「サイコロを振ったときの目」を確率変数 \(X\) としたとき、 \(V[X] = \sum_{i=1}^6{(i - 3.5)^2 * 1/6} = 35 / 12\) です。

条件付き確率¶

「ある事象Bが起こる」という条件のもとで、「事象Aの確率」を 条件付き確率 といい、 \(P(A | B)\) と記述します（ \(P_B(A)\) と書くこともあります）。以下のように定義されます。

\(P(A|B) = \frac{P(A \cap B)}{P(B)}\)

\(A \cap B\) は、 \(A\) と \(B\) の両方とも起こる事象です。たとえば、「6の目が出たら振り直すときの1の目が出る」確率は、事象Bを「5以下の目が出る」、事象Aを「1の目が出る」とすることで、 \(P(A|B) = \frac{1/6}{5/6} = 1/5\) と計算できます。

ベイズの定理¶

\(P(A) > 0\) のときに、条件付き確率に関する以下の式が成り立つことを ベイズの定理 といいます。

\(P(B|A) = \frac{P(A|B) P(B)}{P(A)}\)

確率分布¶

確率分布 （probability distribution）は、確率変数に対して、値とその確率を表したものです。離散確率分布と連続確率分布の2つがあります。

離散確率分布：「値と確率」の集合で定義される分布（以降の例では、離散一様分布、二項分布、負の二項分布、ポアソン分布）
連続確率分布：値に対する確率を表す関数で定義される分布（以降の例では、連続一様分布、正規分布、対数正規分布、指数分布）

SciPyの確率変数¶

以降では、色々な確率分布に対するSciPyの確率変数を示します。主なメソッドを以下に示します。これらは、確率変数クラスのインスタンスメソッドであり、スタティックメソッドでもあります。

メソッド	意味
mean	平均
var	分散
std	標準偏差
pmf	確率密度関数
cdf	累積分布関数（確率密度関数の累積）
rvs	乱数の発生

サイコロに対応する離散一様分布の確率変数を例にサンプルコードを示します。 rvs の結果は、実行ごとに変わります。

import scipy.stats as stats
values = list(range(1, 7))
rv = stats.randint(1, 7)  # 確率変数（インスタンス）

print(rv.mean(), rv.var(), rv.std())  # 3.5, 2.916..., 1.707...

print([rv.pmf(i) for i in values])
# [0.166..., 0.166..., 0.166..., 0.166..., 0.166..., 0.166...]

print([rv.cdf(i) for i in values])
# [0.166..., 0.333..., 0.5, 0.666..., 0.833..., 1.0]

print(rv.rvs(3))  # 3 random values(ex. [3 1 4])

# スタティックメソッド
print(stats.randint.mean(1, 7))  # 3.5
print(stats.randint.var(1, 7))  # 2.916...
print(stats.randint.std(1, 7))  # 1.707...
print([stats.randint.pmf(i, 1, 7) for i in values])
# [0.166..., 0.166..., 0.166..., 0.166..., 0.166..., 0.166...]
print([stats.randint.cdf(i, 1, 7) for i in values])
# [0.166..., 0.333..., 0.5, 0.666..., 0.833..., 1.0]
print(stats.randint.rvs(1, 7, size=3))  # 3 random values(ex. [3 1 4])

離散一様分布¶

離散一様分布は、下限から上限＋１の範囲の整数値をとり、全て同じ確率となる分布です。 stats.randint が対応します。サイコロに対応する確率変数は、 stats.randint(1, 7) です。

参考

二項分布¶

成功か失敗のどちらかの結果になる試行をベルヌーイ試行といいます。独立なN回のベルヌーイ試行を行ったときの成功回数の分布を二項分布といいます。たとえば、「サイコロを10回振ったときに、1の目がでた回数」は二項分布になります。 stats.binom が対応します。

参考

負の二項分布¶

独立なベルヌーイ試行を行ったときに、R回成功するまでの回数の分布を負の二項分布といいます。たとえば、「サイコロの1の目が2回出るまでに振る回数」は負の二項分布になります。 stats.nbinom が対応します。

参考

ポアソン分布¶

「微小な時間にまれに発生する事象」が特定の時間内に発生する回数の分布をポアソン分布といいます。たとえば、「ある範囲の1日の交通事故の件数」はポアソン分布になります。 stats.poisson が対応します。

参考

連続一様分布¶

連続一様分布は、下限から上限の間で同じ確率となる分布です。たとえば、「棒を投げたときに、棒の向きと北の向きの間の角度」が連続一様分布になります。 stats.uniform が対応します。

参考

正規分布¶

独立な多くの確率変数の和は正規分布になります（中心極限定理といいます）。正規分布は自然界に多く見られる重要な分布です。たとえば、「下限0で上限1の連続一様分布」から独立に6個発生した値の和は、ほぼ正規分布になります。 stats.norm が対応します。

参考

対数正規分布¶

ある確率変数 \(X\) が対数正規分布に従うとき、 \(\log X\) は正規分布に従う確率変数になります。負の値を取らないという特徴があります。 stats.lognorm が対応します。

参考

指数分布¶

「微小な時間にまれに発生する事象」が発生する間隔の分布が指数分布になります。指数分布の特徴として、無記憶性があります。 \(X\) を指数分布に従う確率変数とします。このとき、 \(E[X|X\ge 10] = E[X] + 10\) になります。たとえば、ある場所は、タクシーが来るまでの時間が「平均20分の指数分布」とします。9時からタクシーを待ちはじめました。9時の時点でタクシーが来る平均時刻は9:20です。10分待って9:10になったときも、「残りの待ち時間」の平均は20分のままです。すなわち、タクシーが来る平均時刻は9:30です。無記憶性があるので、何分待っても、その時刻からの残りの待ち時間は平均時間と同じです、 stats.expon が対応します。

参考

推測統計学¶

推測統計学とは、母集団の平均などの統計量について、標本から推測する統計学です。詳しくは下記を参照ください。

当コンテンツの知的財産権は株式会社ビープラウドに所属します。詳しくは利用規約をご確認ください。