推測統計学¶
推測統計学とは、母集団の平均などの統計量について、標本から推測する統計学です。
PyQでは、以下の2つを扱っています。
点推定
区間推定
以下の説明では、標本は、リストの変数dataに入っているとします。また、下記のimportをしているものとします。
import numpy as np
from scipy.stats import t, ttest_1samp, ttest_rel, ttest_ind
data = list(何らかの標本)
点推定¶
点推定とは、標本から母集団の分布のパラメーターを推定することです。
母集団が正規分布のとき¶
平均:標本の平均
np.mean(data)で母集団の平均を推定できます。分散:標本の不偏分散
np.var(data, ddof=1)で母集団の分散を推定できます。標準偏差:標本の標準偏差
np.std(data, ddof=1)で母集団の標準偏差を推定できます。
不偏分散¶
標本の(分散などの)統計量の平均が、母集団の統計量に等しい場合、その推定量は不偏性があるといいます。不偏分散とは不偏性のある分散です。
関連クエスト
点推定 - PyQの2問目の解説
母集団が指数分布のとき¶
平均:標本の平均
np.mean(data)で母集団の平均を推定できます。
区間推定¶
点推定では、母集団の統計量を1つの値で推定していました。しかし、その値にぴったり一致することはほぼないでしょう。 1つの値ではなく「下限と上限の範囲」で推定することを区間推定といいます。推定される区間のことを信頼区間といいます。
区間推定では、母集団は正規分布に従うと仮定します。また、推定する統計量は平均とします。平均が未知のデータで分散が既知ということは、あまりないので、「分散は未知」と仮定することが一般的です。以下の説明でも母集団の分散は未知とします。
正規分布に従う母集団から標本サイズnの標本を取ると、平均のばらつきは、自由度n-1のt分布の値が関わってきます。
t分布とは¶
t分布は、母集団の分散が未知のときに、平均の信頼区間を求めるのに使います。スチューデント分布ともいいます。
信頼水準と信頼区間¶
信頼区間は、100%を保証するものではありません。確からしさをどの程度にするかを、分析者が決める必要があります。この確からしさを信頼水準(confidence level)とか信頼係数(confidence coefficient)といいます。
信頼水準としては、95%がよく用いられます。他には、99%や90%を使うこともあります。信頼水準を95%としたとき、その信頼区間を「95%信頼区間」と呼ぶことにします。
95%信頼区間とは¶
「ある標本に対して信頼区間を計算したときに、その区間に母集団の平均が入る可能性が95%」ではありません。 母集団の平均は1つの値であり、1つ信頼区間が決まったときには、その値は入るか入らないかのどちらかで、確率で母集団の平均がばらつくわけではありあせん。
「信頼区間を計算する手順を何度も繰り返したとしたときに、その区間に母集団の平均が入る割合が95%」になります。
信頼区間の計算¶
信頼区間は、下記の式で計算できます。
信頼区間 = 標本平均 - t(n - 1) * sqrt(不偏分散 / n) 〜 標本平均 + t(n - 1) * sqrt(不偏分散 / n)
ただし、nは標本サイズ、t(n - 1)は自由度n - 1のt分布の値です。t分布の自由度は、t分布に必要なパラメーターで、標本サイズ - 1になります。
SciPy.statsでは、t.intervalで、信頼区間の下限loと上限upを計算できます。
第1引数:信頼水準
第2引数:自由度
第3引数:平均
第4引数:sqrt(不偏分散 / 標本サイズ)
a = 0.95 # 信頼水準
n = len(data) # 標本サイズ
m = np.mean(data) # 平均
s2 = np.var(data, ddof=1) # 不偏分散
se = np.sqrt(s2 / n) # 標準誤差
lo, up = t.interval(a, n - 1, m, se) # 信頼区間
またt.ppfで、t分布の値を求めると、以下のようにも計算できます
tvalue = t.ppf((1 + a) / 2, n - 1)
lo = m - tvalue * se
up = m + tvalue * se
信頼水準a(=0.95)の信頼区間を計算したい場合、(1 + a) / 2(=0.975)となるt分布の値を使います。
これは、信頼区間の右側と左側に2.5%ずつあるからです。
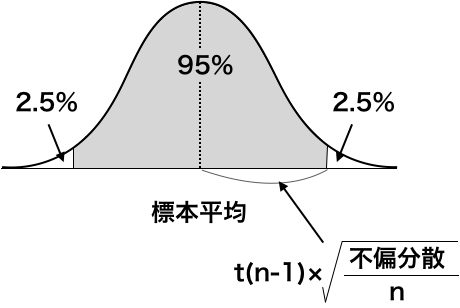
変数se「sqrt(不偏分散 / n)」は標準誤差と同じ式です。
標準誤差とは¶
標本の平均の標準誤差(standard error; SE)とは、サンプリングを無限回、行われたと仮定したときの平均の標準偏差です。標本サイズnと母集団の標準偏差σから次のように計算できます。
SE = σ / sqrt(n)
t分布の色々な関数¶
t.intervalで区間を計算しましたが、他にも色々な関数があります。
関数 |
説明 |
|---|---|
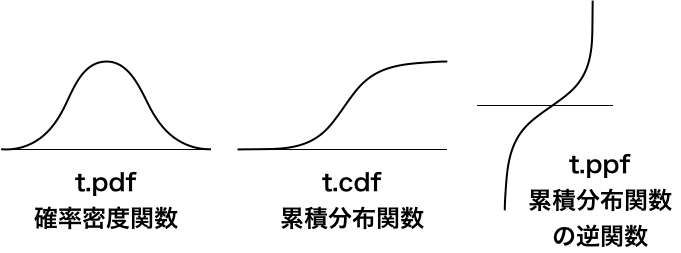
t.pdf |
t分布の確率密度関数 |
t.cdf |
t分布の累積分布関数 |
t.ppf |
t分布の累積分布関数の逆関数 |
仮説検定¶
仮説検定とは、確率的な事柄について、結論を出す手法です。
仮説検定の用語と流れ¶
AとBが同じである(差がない)という仮説を帰無仮説といいます(表記H0が使われます)。
帰無仮説に対立する仮説を対立仮説といいます。主張したいことになります(表記H1が使われます)。
めったに起こらないという判断基準を有意水準といいます。たとえば、5%を使います。
「めったに起こらないことが起こる」→「意味の有ることが起きる」ということで「有意」水準といいます。
帰無仮説が正しいとした仮定とき、観測した事象よりも極端なことが起こる確率をp値といいます。
帰無仮説を捨てて対立仮説を取ることを、帰無仮説を棄却するといいます。
p値とは¶
p値とは、得られたデータが、その値以上にまれなことが起こる確率です。
たとえば、「2個のサイコロの和が11」というデータが得られたとします。 それ以上にまれなことは、下記の3つです。
サイコロの目が、5と6 サイコロの目が、6と5 サイコロの目が、6と6 従って、p値は、3 / 36 = 0.0833になります。
p値が小さいと、「起こる可能性の低いことが起こった」と考えるのではなく、「前提(帰無仮説)が間違ってた」と考えて、帰無仮説を棄却します。
仮説検定の結論¶
有意水準より小さい:帰無仮説が棄却される→対立仮説が正しい 有意水準より大きい:帰無仮説が棄却されない→帰無仮説は正しいとも間違っているともいえない
仮説検定の主張について¶
帰無仮説を「同じでない」とはできません。なぜなら、どのくらい違うのかは、無限に可能性があるため、p値を計算できないからです。 従って、対立仮説「同じである」は(帰無仮説「同じでない」を立てられないので)主張できません。 言えたとしても「『同じである』が間違っているとはいえない」になります。
「違う」というために「同じ」と仮定してから「同じは間違い」というのが、仮説検定です。
主な仮説検定の種類¶
母集団の数や標本の数で以下のように分けられます。
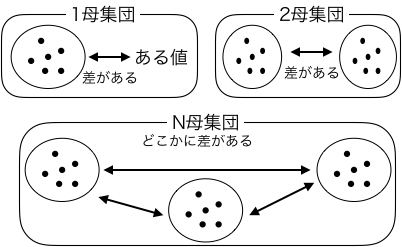
1母集団の平均がある値と異なる
1母集団の1つの標本の平均がある値と異なる
1母集団の1つの標本の平均がある値より大きい
1母集団の1つの標本の平均がある値より小さい
1母集団の2つの標本の平均が異なる
2母集団の2つの標本の平均が異なる
N母集団のN個の標本の平均の中でどれか2つが異なる
「平均がある値と異なる」という主張にも3種類あります(1標本時)。ただし、有意水準に対応するしきい値が違うだけで、本質的には同じです。
平均がある値と差がある:帰無仮説は「平均がある値と同じ」です。両側検定といいます。標本平均が2つのしきい値の外側のときに主張がいえます。
平均がある値より大きい:帰無仮説は「平均がある値以下」です。片側検定といいます。標本平均が1つのしきい値以上のときに主張がいえます。
平均がある値より小さい:帰無仮説は「平均がある値以上」です。片側検定といいます。標本平均が1つのしきい値以下のときに主張がいえます。
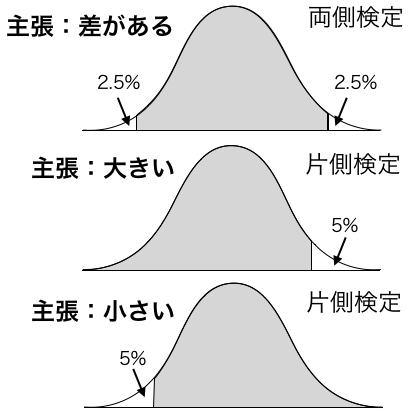
しきい値は、下記のように計算できます。

仮説検定の誤り¶
仮説検定は、確率を扱っているので間違えることもあります。間違え方も次の2通りあります。
\ |
帰無仮説が真 |
帰無仮説が偽 |
|---|---|---|
帰無仮説を棄却しない |
正しく検出 |
間違い(第2種の過誤) |
帰無仮説を棄却する |
間違い(第1種の過誤) |
正しく検出 |
第1種の過誤¶
有意水準をαとします。 帰無仮説が真であっても、αの確率でp値がこの値を下回り、帰無仮説を棄却します。これを第1種の過誤といいます。有意水準は、第1種の過誤を犯す確率そのものです。
たとえば、α=0.05と決めることは、次のように考えたことになります。
「100回に5回は、めったに起こらない」としよう。そうすれば、95回は正しく判断できる。5回は間違えても良い。
第2種の過誤¶
帰無仮説が偽のときに、ある確率(β)でp値がこの値を上回り、帰無仮説を棄却しません。これを第2種の過誤といいます。
帰無仮説が偽のときに正しく棄却できる確率1 - βを検出力といいます。
第1種の過誤と第2種の過誤はトレードオフになっています。
\ |
第1種の過誤 |
第2種の過誤 |
|---|---|---|
有意水準を大きくする |
大きくなる |
小さくなる |
有意水準を小さくする |
小さくなる |
大きくなる |
帰無仮説によって、「2つの過誤のどちらを重視するべきか」は変わるでしょう。 たとえば、帰無仮説が「病気にかかっている」だと、有意水準は小さい方がいいでしょう(ただし、小さすぎても検査ばかりになります)。
第1種の過誤 → 病気を見逃す
第2種の過誤 → 無駄に検査する
「1母集団の1つの標本の平均がある値と差がある」を主張したいとき¶
帰無仮説を「平均がある値と同じ」とします。
ttest_1samp(data, ある値).pvalue < 有意水準 のときに、帰無仮説を棄却します。
「1母集団の1つの標本の平均がある値より大きい」を主張したいとき¶
帰無仮説を「平均がある値以下」とします。
np.mean(data) > ある値 and ttest_1samp(data, ある値).pvalue / 2 < 有意水準 のときに、帰無仮説を棄却します。
「1母集団の1つの標本の平均がある値より小さい」を主張したいとき¶
帰無仮説を「平均がある値以上」とします。
np.mean(data) < ある値 and ttest_1samp(data, ある値).pvalue / 2 < 有意水準 のときに、帰無仮説を棄却します。
「1母集団の2つの標本の平均が異なる」を主張したいとき¶
2つの標本のデータをdata1とdata2とします。
帰無仮説を「2標本の平均が同じ」とします。
ttest_rel(data1, data2).pvalue < 有意水準 のときに、帰無仮説を棄却します。
片側検定の場合は、pvalue / 2と比較します。
「2母集団の2つの標本の平均が異なる」を主張したいとき¶
2つの標本のデータをdata1とdata2とします。
帰無仮説を「2標本の平均が同じ」とします。
ttest_ind(data1, data2, equal_var=False).pvalue < 有意水準 のときに、帰無仮説を棄却します。
equal_var=Falseにより、2つの母集団の分散が等しいと仮定しません。普通は不明なので指定した方がよいでしょう。このオプションを指定したときは、Welchの方法を使います。
データではなく、統計量を使う場合は、以下のようにできます。
ttest_ind_from_stats(平均1, 標準偏差1, 標本サイズ1, 平均2, 標準偏差2, 標本サイズ2, equal_var=False).pvalue < 有意水準
また、片側検定の場合は、pvalue / 2と比較します。
「N母集団のN個の標本の平均の中でどれか2つが異なる」を主張したいとき¶
N個をまとめて扱えませんので、2つずつN×(N - 1) / 2回比較します。
ただし、何度も比較するので、第1種の過誤は、有意水準より大きくなります。それを補正する方法として、有意水準を使うところで、有意水準 / 比較回数を使う方法があります(ボンフェローニ補正)。
それでも、第1種の過誤は有意水準と同じにはなりませんし、第2種の過誤は大きくなります。
また、片側検定の場合は、p値の半分と比較します。

