数理最適化とは¶
数理最適化(以降は単に最適化)とは、数理モデルを用いる手法です。 数理モデル(以降は単にモデル)は、変数と目的関数と制約条件から構成されます。数式を使って表現するので、「数理」ということばが付きます。
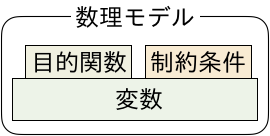
変数:意思決定の対象。
目的関数:評価するための関数。最大化か最小化を選べます。
制約条件:満たすべき条件。
線形最適化とは¶
数理最適化に対し、次の条件がついたものを線形最適化といいます。
変数は、連続変数のみ使えます。連続変数とは、実数値を取る変数です。
目的関数と制約条件の関数は、線形の式(一次式)のみ使えます。一次式とは、一次の変数だけ利用できる式です。
参考:線型計画法(線型計画法は、線形計画法の古い言い方です。また、線形計画法も線形最適化と言い換えるようになってきました。)
線形最適化でできること¶
線形最適化を使うと、社会の色々な問題を解決できます。
意思決定を支援できます。
利益を最大化したり、費用を最小化したりできます。
線形最適化を使った問題解決の手順¶
問題を把握とモデルの設計
モデルの作成
モデルをソルバーで解く
結果の吟味
Pythonの利用¶
最適化を実行する方法として、Pythonはお勧めです。
Pythonで線形最適化を行うには、PuLPライブラリーを使用します。 PuLPは、COIN-ORプロジェクトで開発されたものです。 問題解決の各手順で、以下のようにPythonを用います。
モデルの作成:PuLPライブラリーを利用します。
モデルをソルバーで解く:PuLPから簡単にできます。
結果の吟味:表やグラフで確認します。
参考:COIN-OR
PuLPのインストール¶
コマンドプロンプトで、pip install -U pulpでできます(macOSではpip3 install -U pulp)。
線形最適化のQ&A¶
線形最適化は、使われていますか?
線形最適化は、社会で広く使われています。
無料で使えますか?
モデラーもソルバー(CBC)も特に制限なく無料で使えます。CBCは、PuLPをインストールすると同時にインストールされます。CBCは、Common Public Licenseなので、商用でも利用できます。
大きなサイズも解けますか?
線形最適化は、変数が数十万ぐらいまでであれば、大丈夫でしょう。それ以上であれば、有料のソルバーをお勧めします。

