グラフ理論とNetworkX¶

グラフ理論は、グラフ・ネットワークに関する学問です。

グラフ・ネットワークで扱えること¶

グラフ・ネットワークは、社会の色々なところに現れています。
- 通信ネットワーク
- 物流ネットワーク
- 鉄道ネットワーク
- エネルギーネットワーク
グラフ理論を使うと、以下のような色々な問題を解けます。
- 最短路問題
- 最小全域木問題
- 最小費用流問題
- 最大マッチング問題
- などなど

グラフとは¶

頂点（vertex, node）と辺（edge, arc）からなる構造をグラフ構造（graph）といいます。
- 通常、頂点や辺は、重み（weight）などの属性を持ちます。
辺上にモノを流す場合は、ネットワーク（network）といいます。
- ネットワークでは、辺の重み（weight）を考慮します。

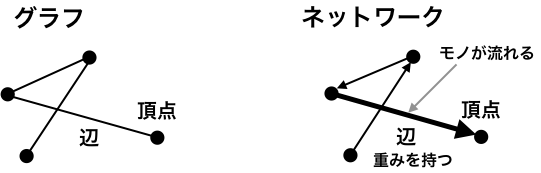
※ PyQでは、折れ線グラフのようなグラフと、頂点と辺からなるグラフの 2 種類に対し、同じグラフという言葉を用いているので、文脈に合わせて適宜解釈してください。

NetworkXとは¶

Pythonでは、グラフ・ネットワークを扱うライブラリーとしてNetworkXがあります。 NetworkXを使うと、色々なアルゴリズムを使えます。

以降では、NetworkXは、import networkx as nxとして使い、nxとして参照します。また、グラフはgで参照します。

参考

NetworkXのインストール¶

コマンドプロンプトで、pip install -U networkxでできます（macOSではpip3 install -U networkx）。

グラフの表記¶

グラフを表記するのに以下の記号を使うことがあります。Vertex, Edge, Graphから来ています。

V：頂点の集合
E：辺の集合
G：グラフ
- VとEからなることを明示的に表す場合、G(V, E)と表記します

NetworkXのグラフの種類¶

NetworkXのグラフには4種類あります。

	無向グラフ	有向グラフ
単純グラフなど※	Graph	DiGraph
多重グラフ	MultiGraph	MultiDiGraph

※ 上表の「単純グラフなど」は、単純グラフ、または自己ループのみ含む多重グラフを指しています。

グラフの用語¶

単純グラフ（simple graph）：自己ループも多重辺も含まないグラフ
多重グラフ（multi graph）：単純グラフとは限らないグラフ
無向グラフ（undirected graph）：無向辺だけからなるグラフ
有向グラフ（directed graph）：有向辺だけからなるグラフ
自己ループ（loop）：両端が同じ頂点となる辺
多重辺（multiple edges）：2つの頂点の間に複数の辺がある場合、それらを多重辺といいます
有向辺（directed edge）: 向きがある辺
無向辺（undirected edge）: 向きのない辺

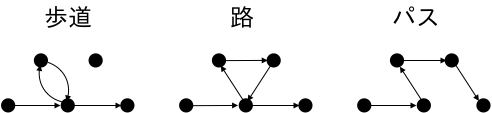
歩道：ある頂点から辺をたどって別の頂点へ行ける場合、その辺の並びを歩道といいます。
路：辺が重複しない歩道を路といいます。
パス：頂点が重複しない路をパス（path）や道といいます。

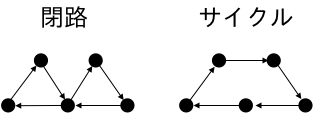
閉路：始点と終点が同じ路を閉路といいます。
サイクル：始点と終点が同じパスをサイクルといいます。

参考

グラフ理論 - 道と閉路
閉路
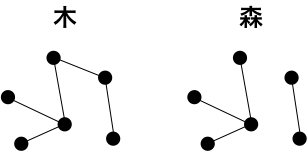
木（tree）：サイクルのないグラフで、連結しているもの。
森（forest）：サイクルのないグラフで、連結しているとは限らないもの。

グラフ描画¶

Jupyter Notebookでは、nx.draw_networkx(グラフオブジェクト)で、簡単にグラフを描画できます。

無向グラフ（Graph）の辺は、線で描画されます。
有向グラフ（Graph）の辺は、矢印で描画されます。

GraphとMultiGraphの違い¶

GraphとMultiGraphの違いは、グラフの辺(u, v)があったときに、以下のようになります。

辺が一意に決まるグラフ：GraphまたはDiGraphで作成できます。
辺が一意に決まらないグラフ：MultiGraphまたはMultiDiGraphで作成できます。

グラフオブジェクトの変換¶

グラフオブジェクトの作成では、他の種類のグラフオブジェクトを引数に取って、種類を変更できます。

g1 = nx.Graph()  # 無向グラフ
g2 = nx.DiGraph(g1)  # 有向グラフに変換

上記のコードは、無向グラフg1を有向グラフに変換しています（g2）。

「無向グラフ → 有向グラフ」は、to_directedメソッドでも変換できます。
- g2 = g1.to_directed()
「有向グラフ → 無向グラフ」は、to_undirectedメソッドでも変換できます。
- g1 = g2.to_undirected()

連結グラフとは¶

2つの頂点の間にパスが存在するとき連結しているといいます。
全ての頂点が連結しているグラフを連結グラフ（connected graph）といいます。
- NetworkXでは、nx.is_connectedでチェックできます。
有向グラフの任意の2点間にパスが存在する場合、強連結といいます。
- NetworkXでは、nx.is_strongly_connectedでチェックできます。
有向グラフが「無向グラフに変換したときに連結である」ならば、弱連結といいます。
- NetworkXでは、nx.is_weakly_connectedでチェックできます。

参考：連結グラフ

グラフの編集¶

add_node(頂点オブジェクト)：頂点の追加
add_edge(頂点オブジェクト1, 頂点オブジェクト2)：辺の追加
頂点オブジェクトは、辞書のキーに使えるものでないといけません。たとえば、数字や文字列が使えます。リストは使えません。
add_nodes_from(頂点リスト)：頂点リストを一括で作成します。
add_edges_from(辺リスト)：辺リストを一括で作成します。

実は、頂点を追加していなくても、いきなり辺の追加ができます。辺を追加するときに、指定された頂点が存在しない場合、自動的に頂点の追加も行われます。

`add_node`で頂点の追加が必要な場合¶

指定した順番に頂点のリストを作成したいとき：辺を追加する前に、順番通りに頂点を追加します。
頂点に属性を設定したいとき：追加時に属性を指定できます。

属性の指定¶

頂点や辺に、任意の属性を指定できます。属性は、頂点や辺の辞書に設定されます。

頂点の追加：add_node(頂点オブジェクト, 頂点の属性1, 頂点の属性2, ...)
辺の追加：add_edge(頂点オブジェクト1, 頂点オブジェクト2, 辺の属性1, 辺の属性2, ...)

補足

属性は、キーワード引数として指定します。いくつでも指定できます。任意のキーワードが使えます。
NetworkXのいくつかの関数では、weightなどの属性を利用しているものがあります。

属性の参照¶

g.nodes[0]とすると、頂点0の辞書を取得できます。
- 属性は、g.nodes[0]['name']のようにアクセスできます。
g[0][1]とすると、辺(0, 1)の辞書を取得できます。
- 属性は、g.edges[0][1]['capacity']のようにアクセスできます。
- g[0][1]の代わりに、g.edges[0, 1]あるいはg.get_edge_data(0, 1)とも書けます。
nx.get_node_attributes(g, 'name')とすると、全頂点のnameの値を辞書で取得できます。
nx.get_edge_attributes(g, 'capacity')とすると、全辺のcapacityの値を辞書で取得できます。
g.nodes.data('name')とすると、全頂点のnameの値をビュー（辞書のようなもの）で取得できます。
g.edges.data('capacity')とすると、全辺のcapacityの値をビュー（タプルのリストのようなもの）で取得できます。

補足

無向グラフに辺(i, j)を追加すると、辺(i, j)としても、辺(j, i)としても、同じものとしてアクセスできます。
- 辺の追加は、g.add_edge(1, 0, capacity=10)で行いましたが、g.edges[0][1]で参照できます。
有向グラフでは、辺(i, j)と辺(j, i)は、別になります。

属性と共に一括作成¶

方法その1

add_edges_fromでは、辞書を指定することもできます。

g = nx.Graph()
g.add_edges_from([(0, 3, {'weight': 10}),
                  (1, 2, {'weight': 15}),
                  (1, 3, {'weight': 20})])

方法その2

属性が1種類のときは、以下のようにadd_weighted_edges_fromを使えます。

g = nx.Graph()
g.add_weighted_edges_from(
    [(0, 3, 10), (1, 2, 15), (1, 3, 20)], 
    weight='weight')

このように、NetworkXでは、柔軟にグラフを作成できます。

頂点の削除¶

remove_node(頂点)：対象の頂点と、その頂点に接続する辺を削除します。
remove_nodes_from(頂点のリスト)：複数の頂点を一括で削除します。

辺の削除¶

remove_edge(辺)：対象の辺を削除します。
remove_edges_from(辺のリスト)：複数の辺を一括で削除します。

ある頂点に接続する全ての辺を削除したとしても、その頂点は削除されません。

色々なグラフの作成¶

nx.path_graph(頂点数)：パスからなるグラフ

nx.cycle_graph(頂点数)：サイクルからなるグラフ

nx.ladder_graph(段数)：はしご状のグラフ

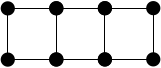
nx.circular_ladder_graph(頂点数)：端がつながったはしご状のグラフ
nx.grid_2d_graph(頂点数1, 頂点数2)：2次元の格子グラフ

ランダムなグラフの作成¶

fast_gnp_random_graph(n, p, seed, directed)：ランダムなグラフの作成
- n：頂点の数
- p：任意の2頂点の間に辺を作成する確率
- seed：乱数シード（指定すると、同じ結果を返します）
- directed：有向グラフかどうか

ランダムな連結グラフの作成

ランダムに作成すると、グラフが連結していない可能性があります。以下のようにすれば、確実に連結グラフを作成できます。

while True:
    g = nx.fast_gnp_random_graph(6, 0.5)
    if nx.is_connected(g):
        break

完全グラフの作成¶

完全グラフとは

全ての頂点間に辺が存在するグラフを完全グラフ（complete graph）といいます。
NetworkXでは、nx.complete_graph(頂点数)で作成できます。
頂点数をnとすると、辺の数はn * (n - 1) // 2で計算できます。

参考：完全グラフ

空グラフの作成¶

空グラフとは

辺のないグラフを空グラフといいます。nx.empty(頂点数)で作成できます。

参考：空グラフ

補グラフの作成¶

補グラフとは

元のグラフに対して、以下のグラフを補グラフ（complement graph）といいます。
- 元のグラフに辺がある → 補グラフの辺を作らない
- 元のグラフに辺がない → 補グラフの辺を作る
NetworkXでは、nx.complement(元のグラフ)で作成できます。

補グラフの補グラフは、元のグラフです。
完全グラフの補グラフは、空グラフです。

参考：補グラフ

2部グラフの作成¶

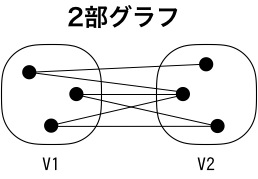
2部グラフとは

頂点集合を2つの集合V1とV2に分けます。
それぞれの集合内について、頂点間に辺がないグラフを2部グラフ（bipartite graph）といいます。
NetworkXでは、nx.bipartiteモジュールに多くの関数が定義されています。

参考：2部グラフ

完全2部グラフの作成¶

完全2部グラフとは

2部グラフで、V1の任意の頂点とV2の任意の頂点の間に辺が存在するグラフを完全2部グラフ（complete bipartite graph）といいます。
NetworkXでは、nx.complete_bipartite_graph(頂点数1, 頂点数2)で作成できます。

参考：完全2部グラフ

完全2部グラフは、割当問題のモデルを作成するときに利用したりします。

参考：割当問題 - ORWiki

格子グラフ¶

grid_2d_graph(m, n)は、m x nの格子グラフを作成します。
頂点は、(i, j)というタプルになります。座標を表します。

編集不可のグラフ¶

関数	説明
nx.freeze(g)	編集不可のグラフ

「凍らせる（freeze）→変更できない」ということです。

逆向きのグラフ¶

有向グラフの向きを反転させます。

関数	説明
nx.reverse(g)	有向グラフの向きを反転したグラフ

reverseは、DiGraphかMultiDiGraphで使えます。

線グラフ¶

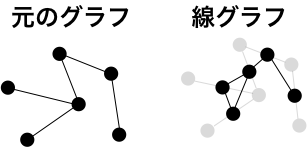
線グラフとは

辺を頂点とみなした新たなグラフ。元のグラフの2辺が頂点を共有していれば、線グラフ（line graph）の対応する頂点間に辺を作成します。

関数	説明
nx.line_graph(g)	線グラフ

line_graphは、GraphかDiGraphで使えます。

線グラフと似ているグラフに双対グラフがあります。

双対グラフとは

平面グラフに対して、「領域を頂点にして、隣接する頂点を辺で結んだグラフ」を双対グラフ（dual graph）といいます。

参考：グラフの双対

平面グラフとは

平面グラフ（plane graph）は、辺が交差しないグラフです。

参考：平面グラフ

線グラフの変換¶

関数	説明
nx.inverse_line_graph(g)	線グラフが元のグラフになるグラフ

line_graphは、Graphのみで使えます。

色々なグラフの作成¶

NetworkXで作成できるグラフの一部を紹介します。

関数	説明
nx.circular_ladder_graph(頂点数)	端がつながったはしご状のグラフ
nx.complete_bipartite_graph(頂点数1, 頂点数2)	完全2部グラフ
nx.complete_graph(頂点数)	完全グラフ
nx.cycle_graph(頂点数)	サイクルグラフ
nx.empty_graph(頂点数)	空グラフ
nx.fast_gnp_random_graph(頂点数, 辺の作成率)	ランダムグラフ
nx.grid_graph(各次元のサイズのリスト)	多次元の格子グラフ
nx.grid_2d_graph(頂点数1, 頂点数2)	2次元の格子グラフ
nx.ladder_graph(頂点数)	はしご状のグラフ
nx.path_graph(頂点数)	1本のパスからなるグラフ
nx.star_graph(頂点数)	スターグラフ

グラフの情報や性質¶

number_of_nodes：頂点数を返します。
number_of_edges：辺数を返します。

頂点ビューと辺ビュー¶

頂点ビュー：頂点のイテレーター。nodes()で取得できます。
- グラフオブジェクトも、頂点のイテレーターです。
辺ビュー：辺のイテレーター。edges()で取得できます。

一般に、ビューとはアクセス用の仮想オブジェクトです。頂点ビューと辺ビューは、イテレーターになっています。頂点や辺で繰り返すときに使えます。

属性つきの頂点ビューと辺ビュー¶

属性つきの頂点ビュー：nodes(data=True)で取得できます。
属性つきの辺ビュー：edges(data=True)で取得できます。
特定の属性つきの頂点ビュー：nodes(data=属性名)で取得できます。
特定の属性つきの辺ビュー：edges(data=属性名)で取得できます。

NetworkXでdataという単語は、頂点や辺の属性を示すときに使われます。

頂点ビューと辺ビューで、引数が不要のときは、プロパティも使えます。

nodes：nodes()と同じです。
edges：edges()と同じです。

無向グラフの接続情報¶

g.neighbors(n)：頂点nの隣接頂点（nと辺で結ばれている頂点）
g.adj[n].items()：頂点nに接続する辺と属性

特定の辺の属性は、get_edge_dataで取得できます。たとえば、辺(1, 2)の属性は、g.get_edge_data(1, 2)で{'weight': 20}になります。

有向グラフの接続情報¶

g.successors(n)：頂点nから出ていく向きの隣接頂点
g.succ[n].items()：頂点nから出ていく辺と属性
g.predecessors(n)：頂点nに入る向きの隣接頂点
g.pred[n].items()：頂点nに入る辺と属性
neighborsは、successorsと同じです。
adjは、succと同じです。
successorは、「後のモノ」という意味です。
predecessorは、「前のモノ」という意味です。

次数とは¶

ある頂点に接続する辺の数を次数（degree）といいます。

全頂点の次数は、g.degree()で辞書のように取得できます。
頂点ndの次数は、g.degree(nd)で取得できます。

無向グラフ、有向グラフの確認¶

関数	性質
nx.is_directed(g)	有向グラフかどうか
g.is_directed()	有向グラフかどうか
not nx.is_directed(g)	無向グラフかどうか
not g.is_directed()	無向グラフかどうか

単純グラフ、多重グラフの確認¶

関数	性質
g.is_multigraph()	`g`の型が多重グラフ用のクラスかどうか
not g.is_multigraph()	`g`の型が単純グラフ用のクラスかどうか

補足

MultiGraph()とMultiDiGraph()は、空のグラフなので単純グラフです。しかし、型がMultiGraphとMultiDiGraphなので、is_multigraph()がTrueになります。

単純グラフは、自己ループや多重辺がないグラフです。しかし、GraphクラスとDiGraphクラスは、自己ループを作成できます。

not g.is_multigraph()は、厳密には、「単純グラフ、または、多重辺のない多重グラフ」となります。

連結しているかどうか¶

関数	関数	性質
無向グラフ	g.is_connected()	連結しているか
有向グラフ	g.is_weakly_connected()	弱連結しているか
有向グラフ	g.is_strongly_connected()	強連結しているか

2部グラフ、空グラフの確認¶

関数	性質
nx.is_bipartite(g)	2部グラフかどうか
nx.is_empty(g)	空グラフかどうか

木、森の確認¶

関数	性質
nx.is_tree(g)	木かどうか
nx.is_forest(g)	森かどうか

パスの確認¶

関数	性質
nx.is_simple_path(g, 頂点リスト)	指定されたリストの隣り合うペアが全て辺に含まれているか

補足

is_simple_pathでチェックするのは、パスです。
- 辺が重複する歩道や、頂点が重複する路は、たとえ全て含まれていてもFalseになります。

オイラー閉路の確認¶

オイラー路、オイラー閉路とは

オイラー路：グラフの全ての辺をちょうど1度だけ通る路
オイラー閉路：グラフの全ての辺をちょうど1度だけ通る閉路

オイラー路であれば、一筆書きで書けます。

オイラー路

関数	性質
nx.is_forest(g)	オイラー閉路かどうか

無向グラフがオイラー閉路かどうかは、下記の定理を使って簡単に調べられます。

オイラーの定理¶

無向グラフがオイラー閉路 ⇔ 連結、かつ、全頂点の次数が偶数

マッチングの確認¶

マッチングとは

互いに端点を共有しない辺の集合をマッチングといいます。
2部グラフのマッチングは、割当問題を解くのに利用したりします。

関数	性質
nx.is_forest(g)	オイラー閉路かどうか

たとえば、2部グラフの左側が男性、右側が女性だとします。複数の相手と付き合っている人がいないとき、マッチングが成立します。

部分グラフとは

グラフG(V, E)に対して、V1 ⊆ V、E1 ⊆ f(E, V1)となるG1(V1, E1)を部分グラフ（subgraph）といいます。
- f(E, V1)は、Eの中で両端がV1に含まれる辺の集合とします。
- NetworkXでは、nx.edge_subgraphで作成できます。
E1 = f(E, V1)の場合、誘導部分グラフ(induced subgraph)といいます。
- NetworkXでは、nx.subgraphで作成できます。

マッチングのチェック方法

マッチングであれば、部分グラフの全頂点の次数が1になります。
is_matching(g, elst1)は、下記のように計算できます。

all(v == 1 for k, v in g.edge_subgraph(elst1).degree())

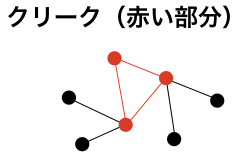
クリークとは

完全グラフになる誘導部分グラフをクリークといいます。

有向非巡回グラフの確認¶

有向非巡回グラフとは

閉路のない有向グラフを有向非巡回グラフ（directed acyclic graph: DAG）といいます。
DAGは、色々なアルゴリズムのデータ構造として使われます。

参考：有向非巡回グラフ

関数	性質
nx.is_directed_acyclic_graph(g)	有向非巡回グラフかどうか

属性を持っているかの確認¶

全ての辺が特定の属性を持っているかどうかは、下記のように確認できます。

関数	性質
nx.is_weighted(g)	全辺が属性`weight`を持っているか

edge：一部の辺で確認したいとき
weight：属性名を'weight'以外にしたいとき

編集不可のグラフかどうか¶

nx.is_frozen(g)で確認できます。

オイラーグラフとサイクル¶

オイラーグラフと準オイラーグラフとは

準オイラーグラフ：オイラー閉路を持つグラフ
オイラーグラフ：オイラー路を持つグラフ

関数	説明
nx.eulerian_circuit(g)	オイラー閉路を取得

オイラー閉路がない場合、nx.NetworkXErrorになります。
オイラー路が欲しい場合は、奇数次数の頂点間にダミーの辺を追加して、オイラー閉路を求めます。

部分的なサイクルの探索¶

部分的なサイクルを探索する関数は、以下のようなものがあります。

関数	対象	説明
nx.find_cycle	無向グラフ、有向グラフ	1つのサイクル（辺リスト）
nx.simple_cycles	有向グラフ	全てのサイクル（頂点リスト）

無向グラフの連結成分¶

関数	説明
nx.connected_components(g)	連結成分（頂点集合）の列挙

connected_componentsは、GraphかMultiGraphで使えます。

connected_componentsでは、頂点集合を列挙します。部分グラフが欲しい場合は、以下のようにしてできます。

for c in nx.connected_components(g):
    sg = g.subgraph(c)  # 部分グラフ
    print(sg.nodes)

有向グラフの連結成分¶

関数	説明
nx.weakly_connected_components(g)	弱連結成分（頂点集合）の列挙
nx.strongly_connected_components(g)	強連結成分（頂点集合）の列挙

上記の関数は、DiGraphかMultiDiGraphで使えます。

有向グラフでは、connected_componentsは使えません。

当コンテンツの知的財産権は株式会社ビープラウドに所属します。詳しくは利用規約をご確認ください。

グラフ理論とNetworkX¶

グラフ・ネットワークで扱えること¶

グラフとは¶

NetworkXとは¶

NetworkXのインストール¶

グラフの表記¶

NetworkXのグラフの種類¶

グラフの用語¶

グラフ描画¶

GraphとMultiGraphの違い¶

グラフオブジェクトの変換¶

連結グラフとは¶

グラフの編集¶

add_nodeで頂点の追加が必要な場合¶

属性の指定¶

属性の参照¶

属性と共に一括作成¶

頂点の削除¶

辺の削除¶

色々なグラフの作成¶

ランダムなグラフの作成¶

完全グラフの作成¶

空グラフの作成¶

補グラフの作成¶

2部グラフの作成¶

完全2部グラフの作成¶

格子グラフ¶

編集不可のグラフ¶

逆向きのグラフ¶

線グラフ¶

線グラフの変換¶

色々なグラフの作成¶

グラフの情報や性質¶

頂点ビューと辺ビュー¶

属性つきの頂点ビューと辺ビュー¶

無向グラフの接続情報¶

有向グラフの接続情報¶

次数とは¶

無向グラフ、有向グラフの確認¶

単純グラフ、多重グラフの確認¶

連結しているかどうか¶

2部グラフ、空グラフの確認¶

木、森の確認¶

パスの確認¶

オイラー閉路の確認¶

オイラーの定理¶

マッチングの確認¶

有向非巡回グラフの確認¶

属性を持っているかの確認¶

編集不可のグラフかどうか¶

オイラーグラフとサイクル¶

部分的なサイクルの探索¶

無向グラフの連結成分¶

有向グラフの連結成分¶

`add_node`で頂点の追加が必要な場合¶