双対問題¶
双対問題とは¶
ある1つの最適化問題に対して、双対問題を考えられます。
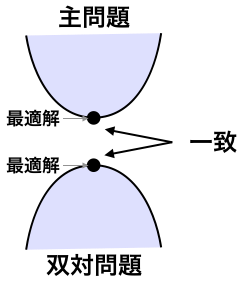
元の問題を主問題といいます。
主問題が最小化問題のとき、双対問題は最大化問題になります。
主問題が最大化問題のとき、双対問題は最小化問題になります。
主問題の変数は双対問題の制約条件に、主問題の制約条件は双対問題の変数に対応します。
双対問題の重要な性質¶
主問題または双対問題のどちらかが最適解を持つならば、もう片方の問題も最適解を持ち、両方の最適解の値は一致します(双対定理)。
補足
双対問題は、線形最適化問題以外でも考えられますが、ここでは線形最適化問題に対する双対問題を考えます。
PuLPよる表現¶

上図左側の主問題は、PuLPで下記のように書けます。
primal_model = LpProblem(sense=LpMaximize)
primal_model += lpSum(c.T * x)
for row, rhs in zip(A, b):
primal_model += lpSum(row * x) <= rhs
また、図右側の双対問題は、下記のように書けます。
dual_model = LpProblem()
dual_model += lpSum(b.T * y)
for row, rhs in zip(A.T, c):
dual_model += lpSum(row * y) >= rhs
図のA x ≦ bのような表現を行列表現といいます。
Aが行列で、b, c, x, yは列ベクトルです。A^TはAの転置を表し、PythonではA.Tと表現しています。
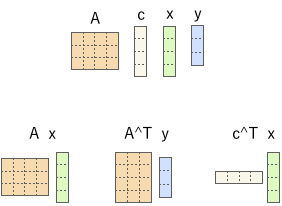
行列表現をコードにするときは、行列の行ごとにforでループする必要があります。
双対問題は、何の役に立つの?¶
双対というのは、数学や物理で重要な概念です。
双対問題の解から、主問題の解を構築できます。
ソルバーによっては、主問題より双対問題の方が解きやすいことがあります。
アルゴリズムによっては、主問題と双対問題を同時に解く方法があります(主双対内点法)。
効用の最大化(主問題)と費用の最小化(双対問題)の最適解が同じであることから、知見を得られます。
参考:双対
双対問題は、どうやって求めるの?¶
ラグランジュ緩和問題を使って求められます。
手順の一部のイメージは、下記のようになります。
b^T y = y^T b ≧ y^T A x = (A^T y)^T x ≧ c^T x
より詳しい説明については、下記書籍などにあります。
dualライブラリー¶
どんな主問題に対しても、双対問題を考えられます。

ある主問題が、どのような双対問題になるのか覚えるのは大変です。
dualライブラリーを使うと、簡単な形式で、双対問題をJupyter上で確認できます。
dualのインストール¶
コマンドプロンプトで、pip install -U dualでできます(macOSではpip3 install -U dual)。
dualの書き方¶
import dualが必要ですセルの最初に
%%dualを書いてくださいモデルの1行目は下記のどちらかを書いてください
min 目的関数の式max 目的関数の式
2行目以降は、下記のように制約条件を書きます
式 >= 定数式 = 定数式 <= 定数
制約条件では、行列形式も使えます。
式の中で、
c^T xのように、左に係数を、右に変数を書きますc^Tは、ベクトルまたは行列cの転置を表します。
サンプル¶
PuLPとの比較を載せます。
import numpy as np
from pulp import LpProblem, LpVariable, lpSum
A = np.array([[1, 0], [0, 1]])
b = np.array([1, 1])
c = np.array([1, 1])
# 主問題
primal_model = LpProblem(sense=LpMaximize)
x = [LpVariable(f'x{i}', lowBound=0) for i in range(2)]
primal_model += lpSum(c.T * x)
for row, rhs in zip(A, b):
primal_model += lpSum(row * x) <= rhs
上記は、下記のように記述します。
%%dual
max c^T x
A x <= b
x >= 0
実行すると、双対問題は、下記のように出力されます。
min b^T y
A^T y >= c
y >= 0
下記と対応します。
# 双対問題
dual_model = LpProblem()
y = [LpVariable(f'y{i}', lowBound=0) for i in range(2)]
dual_model += lpSum(b.T * y)
for row, rhs in zip(A.T, c):
dual_model += lpSum(row * y) >= rhs

